Câu 4.
Cho AB là đường kính của đường trong tâm O. Lấy điểm C trên đường tròn sao cho góc BOC bằng \(60^\circ \). Hãy chọn độ dài của dây cung AC (đơn vị cm) khi đường kính đường tròn bằng 5 cm:
(A) 3 (B) \(3\sqrt 3 \)
(C) \(\dfrac{{5\sqrt 2 }}{2}\) (D) \(\dfrac{{5\sqrt 3 }}{2}\)
Khoanh tròn vào chữ cái trước kết quả đúng
Phương pháp giải:
+ Ta chỉ ra tam giác \(BOC\) đều để tính \(\widehat {CBO},\,\) cạnh \(BC.\)
+ Chứng minh tam giác \(ABC\) vuông tại \(C\) và sử dụng định lý Pytago để tính \(AC.\)
Lời giải chi tiết:
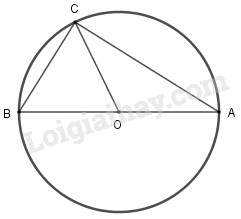
Xét đường tròn \(\left( O \right)\) có \(OB = OC\) và \(\widehat {BOC} = 60^\circ \) nên tam giác \(OBC\) đều, suy ra \(\widehat {CBO} = 60^\circ ;BC = OB = OC = R\)
Lại có tam giác \(ABC\) có ba đỉnh nằm trên \(\left( O \right)\) và có \(AB\) là đường kính nên \(\Delta ABC\) vuông tại \(C.\)
Từ đề bài ta có \(AB = 2R = 5cm \Rightarrow R = \dfrac{5}{2}cm = BC\)
Theo định lý Pytago trong tam giác vuông \(ABC\) ta có \(AC = \sqrt {A{B^2} - B{C^2}} = \sqrt {{5^2} - {{\left( {\dfrac{5}{2}} \right)}^2}}\)
\( = \sqrt {\dfrac{{75}}{4}} = \dfrac{{5\sqrt 3 }}{2}\) cm.
Chọn C.
Câu 5.
Xem hình 8. Hãy viết giải thiết và kết luận của mệnh đề sau: Với hai cung nhỏ trong một đường tròn, cung lớn hơn căng dây lớn hơn và ngược lại.
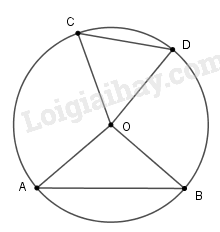
Giả thiết và kết luận như mệnh đề được viết như sau:
a) \(\overparen{AB}\)\( > ... \Rightarrow AB > ...\)
b) \(AB > ... \Rightarrow \)\(\overparen{AB}\)\( > ... \)
Phương pháp giải:
Xác định yếu tố cho trước của mệnh đề để viết giả thiết, xác định điều cần chứng minh để viết kết luận
Lời giải chi tiết:
a) \(\overparen{AB}>\overparen{CD}\)\( \Rightarrow AB > CD\)
b) \(AB > CD\Rightarrow \)\(\overparen{AB}>\overparen{CD}\)
Câu 6.
Hãy điền những từ thích hợp vào chỗ trống (…) trong câu sau:
Trong một đường tròn, hai cung bị chắn giữa………song song………
Phương pháp giải:
Sử dụng tính chất mở rộng: “ Trong một đường tròn, hai cung bị chắn giữa hai dây song song thì bằng nhau”
Lời giải chi tiết:
Trong một đường tròn, hai cung bị chắn giữa hai dây song song thì bằng nhau.
soanvan.me
