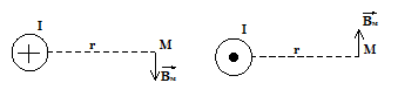PHƯƠNG PHÁP GIẢI BÀI TẬP TỪ TRƯỜNG CỦA DÒNG ĐIỆN TRONG DÂY DẪN CÓ HÌNH DẠNG ĐẶC BIỆT

I- TỪ TRƯỜNG CỦA DÒNG ĐIỆN THẲNG DÀI VÔ HẠN

Đường sức từ của dòng điện thẳng dài vô hạn là những đường tròn đồng tâm.

\(\overrightarrow B \) có:

+ Điểm đặt: Đặt tại điểm đang xét

+ Phương: Vuông góc với bán kính

+ Chiều: Được xác định theo các cách:

  • Quy tắc bàn tay phải: Để bàn tay phải sao cho ngón cái nằm dọc theo dây dẫn và chỉ theo chiều dòng điện, khi đó các ngón kia khum lại cho ta chiều của đường sức từ => xác định được chiều \(\overrightarrow B \)

+ Độ lớn: \(B = {2.10^{ - 7}}\dfrac{I}{r}\) (r - khoảng cách từ điểm đang xét đến tâm)

II- TỪ TRƯỜNG CỦA DÒNG ĐIỆN TRÒN

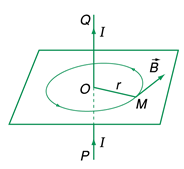
Đường sức từ của dòng điện tròn có phương vuông góc với mặt phẳng vòng dây

\(\overrightarrow B \) có:

+ Điểm đặt: Tại tâm của dòng điện tròn

+ Phương: Vuông góc với mặt phẳng vòng dây

+ Chiều:

  • Quy tắc cái đinh ốc
  • Quy tắc bàn tay phải
  • Quy đi vào mặt S (nam) và đi ra mặt N (bắc): ta thấy chiều của dòng điện cùng chiều quay của kim đồng hồ thì đó là mặt nam, ngược lại là mặt bắc

+ Độ lớn: \(B = 2\pi {.10^{ - 7}}\dfrac{I}{R}\) ( R- bán kính của dòng điện tròn)

III- TỪ TRƯỜNG CỦA DÒNG ĐIỆN TRONG ỐNG DÂY

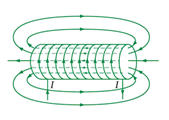
\(\overrightarrow B \) trong lòng ống dây có:

+ Phương : song song trục ống dây

+ Chiều: Xác định theo quy tắc cái đinh ốc

+ Độ lớn: \(B = 4\pi {.10^{ - 7}}\dfrac{N}{l}I\)

Trong đó:

  • N: số vòng dây của ống
  • \(l\): chiều dài ống

IV- NGUYÊN LÍ CHỒNG CHẤT CỦA TỪ TRƯỜNG

\(\overrightarrow {{B_M}}  = \overrightarrow {{B_1}}  + \overrightarrow {{B_2}}  + ... + \overrightarrow {{B_n}} \)

Trong đó:

  + \(\overrightarrow {{B_1}} ,\overrightarrow {{B_2}} ,...,\overrightarrow {{B_n}} \): gọi là véctơ cảm ứng từ do các dòng điện I1, I2,..., In gây ra tại M

  + Đơn vị của cảm ứng từ (B) là : T (tesla)

 V- PHƯƠNG PHÁP CHUNG GIẢI BÀI TẬP XÁC ĐỊNH CẢM ỨNG TỪ

- Bước 1: Xác định hướng của các véctơ cảm ứng từ B do nhiều dòng điện gây ra tại điểm ta đang xét bằng các quy tắc (cái đinh ốc, bàn tay phải, ...) đã nêu ở trên

- Bước 2: Sử dụng nguyên lí chồng chất của từ trường tại điểm đang xét.

\(\overrightarrow {{B_M}}  = \overrightarrow {{B_1}}  + \overrightarrow {{B_2}}  + ... + \overrightarrow {{B_n}} \) (1)

- Bước 3: Đưa phương trình (1) trở về phương trình đại số bằng các cách sau:

+ Chọn hệ trục tọa độ để chiếu

+ Vận dụng phương pháp hình học và các hệ thức lượng trong tam giác thường (định lí hàm số cos, hàm số sin, ... ) và các hệ thức lượng trong tam giác vuông

- Bước 4: Tìm ẩn số của bài toán

Chú ý: Có thể dùng kí hiệu sau để vẽ hình (\( \oplus \)) đi vào, (\( \odot \)) đi ra