Dạng 1: Điện phân có dương cực tan
- Khi có hiện tượng dương cực tan, dòng điện trong chất điện phân tuân theo định luật Ôm giống như đoạn mạch chỉ có điện trở thuần R (vì khi đó có một cực bị tan nên bình điện phân xem như một điện trở).
- Sử dụng định luật Faraday:
+ Định luật I: Khối lượng m của chất được giải phóng ra ở điện cực tỉ lệ với điện lượng q chạy qua bình điện phân đó:
Biểu thức: \(m = kq\) (1)
Trong đó: k (kg/C) gọi là đương lượng điện hóa phụ thuộc vào bản chất của các chất được giải phóng.
+ Định luật II: Đương lượng điện hóa của một nguyên tố tỉ lệ với đương lượng gam \(\frac{A}{n}\) của nguyên tố đó.
Biểu thức: \(k = c\frac{A}{n} = \frac{A}{{Fn}}\) (2) với \(F = \frac{1}{c} = 96500C/mol\)
- Kết hợp (1) và (2) ta có biểu thức định luật Faraday:
\(m = kq = \frac{1}{F}\frac{A}{n}q = \frac{1}{F}\frac{{AIt}}{n}\)
Dạng 2: Điện phân không có dương cực tan
- Khi không có hiện tượng dương cực tan thì bình điện phân xem như một máy thu điện nên dòng điện qua bình điện phân tuân theo định luật Ômm cho đoạn mạch chứa máy thu.
\(I = \frac{{E - {E_p}}}{{r + {r_p}}}\)
- Để giải ta sử dụng:
+ Biểu thức định luật Faraday: \(m = kq = \frac{1}{F}\frac{A}{n}q = \frac{1}{F}\frac{{AIt}}{n}\)
+ Khối lượng riêng: \(D = \frac{m}{V}\)
+ Thể tích: \(V = S.d\)
Trong đó:
D: khối lượng riêng (kg/m3)
d: bề dày kim loại bám vào điện cực (m)
S: diện tích mặt phủ của tấm kim loại (m2)
V: thể tích kim loại bám vào điện cực (m3)
Bài tập ví dụ:
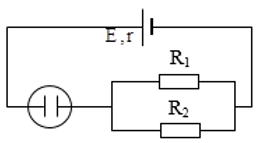
Cho mạch điện như hình vẽ có \(\left( {E,r} \right) = \left( {12V;0,4\Omega } \right)\), \({R_1} = 9\Omega ,{R_2} = 6\Omega \) và một bình điện phân đựng dung dịch CuSO4, anôt bằng Cu và điện trở của bình điện phân \({R_p} = 4\Omega \). Tính:
a) Cường độ dòng điện chạy qua mạch chính.
b) Khối lượng đồng thoát ra ở cực dương trong 16 phút 5 giây.
Hướng dẫn giải
Khi điện phân một dung dịch muối mà kim loại anôt làm bằng chính kim loại ấy thì xảy ra hiện tượng cực dương tan.
a)
Ta có: Rp nt(R1 // R2 )
Suy ra điện trở tương đương của mạch ngoài là:
\(R = \frac{{{R_1}{R_2}}}{{{R_1} + {R_2}}} + {R_p} = \frac{{9.6}}{{9 + 6}} + 4 = 7,6\Omega \)
Cường độ dòng điện qua mạch chính:
\(I = \frac{E}{{R + r}} = \frac{{12}}{{7,6 + 0,4}} = 1,5A\)
b)
Khối lượng Cu thoát ra ở cực dương là:
\(m = \frac{1}{F}\frac{{AIt}}{n} = \frac{1}{{96500}}.\frac{{64.1,5.\left( {16.60 + 5} \right)}}{2} = 0,48g\)