.jpg)
Số dư của phép chia $45{\rm{ }}:{\rm{ }}6$ là
A. $3$
B. $4$
C. $5$
A. $3$
Thực hiện phép chia và xác định số dư của phép chia đó.
$45{\rm{ }}:{\rm{ }}6{\rm{ }} = {\rm{ }}7$ (dư $3$)
Số dư của phép chia bằng $3$.
Đáp án cần chọn là A.
Điền số thích hợp vào chỗ trống:
Nếu lấy một số có hai chữ số nào đó chia cho $5$ thì số dư lớn nhất có thể là số nào ?
Số dư lớn nhất có thể là số
Số dư lớn nhất có thể là số
Trong một phép chia có dư, số dư lớn nhất có thể luôn bé hơn số chia một đơn vị.
Số dư lớn nhất có thể trong phép chia cho $5$ là $4$.
Số cần điền vào chỗ trống là $4$.
.jpg)
Trong một phép chia có dư, số chia là $6$ thì số dư bé nhất có thể là:
A. \(0\)
B. \(1\)
C. \(2\)
D. \(3\)
B. \(1\)
Xác định giá trị của số dư bé nhất trong phép chia có dư rồi chọn đáp án thích hợp.
Trong một phép chia có dư, số chia là $6$ thì số dư bé nhất có thể là: $1$.
Đáp án cần chọn là B.
Có $15$ người khách muốn đi đò sang sông. Mỗi chuyến đò chở được $5$ người, kể cả người lái đò. Cần ít nhất số chuyến đò để chở hết số người đó qua sông là:
A. $3$ chuyến đò
B. $4$ chuyến đò
C. $5$ chuyến đò
D. $6$ chuyến đò.
B. $4$ chuyến đò
- Tìm số khách một chuyến đò chở được.
- Làm phép chia \(15\) với số khách một chuyến đò chở được.
- Nếu còn dư người thì cần thêm một thuyền nữa để chở hết số khách đó.
Mỗi chuyến đò chở được số khách là:
$5{\rm{ }}-{\rm{ }}1{\rm{ }} = {\rm{ }}4$ (người)
Thực hiện phép chia ta có:
$15{\rm{ }}:{\rm{ }}4{\rm{ }} = {\rm{ }}3$ (dư $3$)
Nếu $3$ chuyến đò, mỗi chuyến đò chở $4$ người khách thì còn $3$ người khách chưa sang sông nên cần thêm $1$ chuyến đò nữa.
Vậy cần ít nhất số chuyến đò là:
$3{\rm{ }} + {\rm{ }}1{\rm{ }} = {\rm{ }}4$ (chuyến đò)
Đáp số: $4$ chuyến đò.
Phép chia nào dưới đây có cùng số dư với phép chia $31{\rm{ }}:{\rm{ }}5$ ?
A. \(16:4\)
B. \(19:3\)
C. \(32:6\)
D. \(25:2\)
B. \(19:3\)
D. \(25:2\)
- Làm phép chia $31{\rm{ }}:{\rm{ }}5$ để xác định số dư.
- Lần lượt tính các phép chia trong 4 đáp án, tích vào các phép chia nào có cùng số dư với số dư em vừa tìm được ở bước trên.
Ta có: $31{\rm{ }}:{\rm{ }}5{\rm{ }} = {\rm{ }}6$ (dư $1$)
Và:
$A.{\rm{ }}16{\rm{ }}:{\rm{ }}4{\rm{ }} = 4$
$B.{\rm{ }}19{\rm{ }}:{\rm{ }}3{\rm{ }} = 6$ (dư $1$)
$C.{\rm{ }}32{\rm{ }}:{\rm{ }}6{\rm{ }} = {\rm{ }}5$ (dư $2$)
$D.{\rm{ }}25{\rm{ }}:{\rm{ }}2{\rm{ }} = {\rm{ }}12$ (dư $1$)
Như vậy có hai phép tính có cùng số dư với phép chia đã cho.
Đáp án cần chọn là B và D.
Điền số thích hợp vào chỗ trống:
$38{\rm{ }}:{\rm{ }}4{\rm{ }} = {\rm{ }}9$ (dư
)
$38{\rm{ }}:{\rm{ }}4{\rm{ }} = {\rm{ }}9$ (dư
)
Thực hiện phép chia và điền số dư thích hợp vào chỗ trống.
Ta có: $38{\rm{ }}:{\rm{ }}4{\rm{ }} = {\rm{ }}9$ (dư $2$)
Số cần điền vào chỗ trống là $2$.
Một phép chia có số chia là $6$, thương bằng $18$ và số dư là số dư lớn nhất có thể.
Số bị chia của phép chia đó là:
Số bị chia của phép chia đó là:
- Tìm số dư của phép chia.
- Trong phép chia có dư, muốn tìm số bị chia ta lấy thương nhân với số chia rồi cộng với số dư.
Phép chia có số chia là \(6\) nên số dư lớn nhất có thể là $5$.
Số bị chia của phép chia đó là:
$18{\rm{ }} \times {\rm{ }}6{\rm{ }} + {\rm{ }}5{\rm{ }} = 113$
Đáp số: $113$.
Số cần điền vào chỗ trống là \(113\).
Một số chia cho $5$ thì được $4$ (dư $3$).
Muốn phép chia đó không còn dư nữa thì số bị chia cần bớt đi ít nhất
đơn vị hoặc tăng ít nhất
đơn vị.
Muốn phép chia đó không còn dư nữa thì số bị chia cần bớt đi ít nhất
đơn vị hoặc tăng ít nhất
đơn vị.
- Tìm số bị chia đã cho bằng thương nhân số chia cộng số dư.
- Tìm số đơn vị cần bớt đi ít nhất hoặc số đơn vị cần tăng lên ít nhất để phép chia thành phép chia hết.
Số đã cho là: $4 \times 5 +3=23$
Số $23$ cần bớt đi ít nhất $3$ đơn vị hoặc tăng lên ít nhất $2$ đơn vị thì phép chia sẽ hết.
Ta lần lượt điền số $3$ và $2$ vào các ô trống.
Chia một số cho $5$ thì được thương là số liền sau của số nhỏ nhất có hai chữ số giống nhau và số dư là số dư lớn nhất có thể có.
Vậy chia số đó cho $3\;$ thì có số dư là
Vậy chia số đó cho $3\;$ thì có số dư là
- Tìm thương và số dư trong phép chia cho $5$.
- Tìm số bị chia bằng thương nhân số chia cộng với số dư.
- Tìm số dư khi chia số đó cho $3$ và điền vào chỗ trống.
Số nhỏ nhất có hai chữ số giống nhau là $11$, nên số liền sau của số nhỏ nhất có hai chữ số giống nhau là $12$.
Do đó, thương của phép chia này là $12$.
Số chia của phép chia đó là $5$ nên số dư lớn nhất có thể bằng $4$.
Số bị chia của phép chia đó là: $12{\rm{ }} \times {\rm{ }}5{\rm{ }} + {\rm{ }}4{\rm{ }} = {\rm{ }}64$
Ta có: $64{\rm{ }}:{\rm{ }}3{\rm{ }} = {\rm{ }}21$ (dư $1$)
Số dư của phép chia số đó cho cho $3$ là $1$.
Số cần điền vào chỗ trống là $1$.
Cho phép chia có số chia và thương đều bằng nhau và đều là số lẻ có một chữ số, số dư của phép chia đó là $7$. Số bị chia của phép chia đó là:
A. \(88\)
B. \(86\)
C. \(72\)
D. \(81\)
A. \(88\)
- Tìm số chia và thương; số chia luôn lớn hơn số dư.
- Tìm số bị chia bằng cách lấy thương nhân với số chia, cộng thêm số dư.
Số chia và thương của phép chia là $9$ vì $9$ là số lẻ có $1$ chữ số và lớn hơn số dư.
Số bị chia của phép chia đó là:
$9{\rm{ }} \times {\rm{ }}9\; + {\rm{ }}7{\rm{ }} = {\rm{ }}88$
Đáp số: $88$.
Đáp án cần chọn là A.
Trong một phép chia có dư ta có:
Số dư luôn bằng số chia
Số dư luôn lớn hơn số chia
Số dư luôn bé hơn số chia
Số dư nhỏ nhất là \(1\)
Số dư luôn bé hơn số chia
Số dư nhỏ nhất là \(1\)
- Nhẩm lại mối quan hệ giữa số dư và số chia trong một phép chia; số dư bé nhất có thể.
- Tích vào ô trống đứng trước các đáp án đúng.
- Trong một phép chia có dư, số dư luôn bé hơn số chia.
- Phép chia có dư thì số dư bé nhất bằng \(1\).
Vậy hai nhận xét cuối cùng là đúng.
Cho bài toán theo tóm tắt sau:
$3m$ vải : $1$ bộ quần áo
$65m$ vải: ... bộ quần áo? Thừa … \(m\) vải ?
Đáp án đúng của bài toán này là:
A. $21$ bộ
B. $22$ bộ, thừa $1$ m vải
C. $21$ bộ, thừa $2$m vải
D. $20$ bộ, thừa $5$m vải
C. $21$ bộ, thừa $2$m vải
Chia $65$ cho $3$ để tìm số bộ quần áo may được và số mét vải còn thừa.
Ta có: $65{\rm{ }}:{\rm{ }}3{\rm{ }} = {\rm{ }}21$ (dư $2$)
Vậy có $65m$ vải thì may được nhiều nhất $21$ bộ quần áo và còn thừa $2$ mét vải.
Đáp số: $21$ bộ, thừa $2$m vải.
Đáp án cần chọn là C.
Phép chia nào sau đây là phép chia có dư ?
A. \(20:5\)
B. \(13:2\)
C. \(30:3\)
D. \(36:4\)
B. \(13:2\)
Thực hiện các phép chia đã cho và chọn đáp án có phép chia có dư.
A. ${\rm{ }}20{\rm{ }}:{\rm{ }}5{\rm{ }} = {\rm{ }}4$
B. ${\rm{ }}13{\rm{ }}:{\rm{ }}2{\rm{ }} = {\rm{ }}6$ (dư $1$)
C. ${\rm{ }}30{\rm{ }}:{\rm{ }}3{\rm{ }} = {\rm{ }}10$
D. ${\rm{ }}36{\rm{ }}:{\rm{ }}4{\rm{ }} = {\rm{ }}9$
Vây phép chia có dư là phép chia số $2$.
Đáp án cần chọn là B.
Cho phép chia sau:
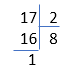
Đáp án nào sau đây sai ?
A. $17{\rm{ }}:{\rm{ }}2{\rm{ }} = {\rm{ }}8$ (dư $1$)
B. $ {\rm{ }}17{\rm{ }} = {\rm{ }}8{\rm{ }} \times {\rm{ }}2{\rm{ }} + {\rm{ }}1$
C. \(17 - 1 = 8 \times 2\)
D. \(17:2 = 8\)
D. \(17:2 = 8\)
- Từ phép chia hàng dọc, ta có thể biểu diễn mối quan hệ của các số.
- Trong phép chia A cho B được thương là Q và số dư R thì ta luôn có: $A{\rm{ }}:{\rm{ }}B{\rm{ }} = {\rm{ }}Q$ (dư $R$) hoặc $A{\rm{ }} = {\rm{ }}B{\rm{ }} \times {\rm{ }}Q{\rm{ }} + {\rm{ }}R.$
A. Đúng
B. Đúng
C. Đúng
D. Sai, vì viết thiếu số dư của phép chia.
Đáp án cần chọn là D.
.jpg)
Đúng ghi Đ, sai ghi S vào ô trống:
$19{\rm{ }}:{\rm{ }}3{\rm{ }} = {\rm{ }}6$ (dư $1$)
$58{\rm{ }}:{\rm{ }}5{\rm{ }} = {\rm{ }}11$ (dư $4$)
$19{\rm{ }}:{\rm{ }}3{\rm{ }} = {\rm{ }}6$ (dư $1$)
$58{\rm{ }}:{\rm{ }}5{\rm{ }} = {\rm{ }}11$ (dư $4$)
Thực hiện các phép chia và kiểm tra kết quả, số dư của mỗi câu có đúng không.
$19{\rm{ }}:{\rm{ }}3{\rm{ }} = {\rm{ }}6$ (dư $1$) là đúng
$58{\rm{ }}:{\rm{ }}5{\rm{ }} = {\rm{ }}11$ (dư $4$) là sai vì $58{\rm{ }}:{\rm{ }}5{\rm{ }} = {\rm{ }}11$ (dư $3$)
Điền số thích hợp vào ô trống:
\(31\,\, = \,\,6\,\, \times \)
$+$
\(31\,\, = \,\,6\,\, \times \)
$+$
Thực hiện phép chia $31$ cho $6$ để tìm được số cần điền vào hai chỗ trống.
Vì $31:6=5$ (dư $1$) nên có thể viết thành:
\(31=6\times5+1\)
Vậy hai số cần điền vào chỗ trống là $5$ và $1.$
.png)
Biết: $x{\rm{ }}:{\rm{ }}3{\rm{ }} = {\rm{ }}9$ (dư $2$). Giá trị của $x$ là:
A. \(21\)
B. \(33\)
C. $29$
D. \(25\)
C. $29$
Trong phép chia có dư, số bị chia được tìm bằng cách lấy thương nhân với số chia rồi cộng với số dư .
$x{\rm{ }}:{\rm{ }}3{\rm{ }} \,\,\,\,= {\rm{ }}9$ (dư $2$).
$\begin{array}{l}x\,\,\,\,\,\,\,\,\,\,\, = 9 \times 3 + 2\\x\,\,\,\,\,\,\,\,\,\,\, = \,\,\,\,\,27 + 2\\x\,\,\,\,\,\,\,\,\,\,\, = \,\,\,\,\,\,\,\,\,\,29\end{array}$