2 đa thức nào sau đây có tổng bằng đa thức K(x) = x3 – 8
-
A
A(x) = x4 + 2x2 + x – 4 và B(x) = x4 + x3 + 2x – 4
-
B
A(x) = x5 – 3x3 -2 và B(x) = - x5 - 4x3 + 6
-
C
A(x) = 3. x3 -2 và B(x) = –2. x3 - 6
-
D
A(x) = 2 và B(x) = x3 – 4x2 – 10
Đáp án của giáo viên lời giải hay : C
Tính tổng của 2 đa thức ở từng đáp án. Tổng của 2 đa thức nào bằng đa thức K(x) = x3 – 8 thì đó là đáp án cần chọn
Ta thấy đa thức 3. x3 -2 + (–2. x3 – 6) = 3x3 – 2x3 + (-2 – 6) = x3 - 8
Cho 2 đa thức A(x) = x2022 – x2020 + x2018 – x2016 + ... + x2 – 1
B(x) = -x2023 + x2021 – x2019 + x2017 - ... – x3 + x
Tìm giá trị của đa thức A(x) – B(x) tại x = -1
-
A
2024
-
B
-2024
-
C
0
-
D
1
Đáp án của giáo viên lời giải hay : C
Tính A(x) – B(x)
Thay giá trị x = -1 vào đa thức hiệu mới tìm được
Ta có: P(x) = A(x) – B(x) = x2022 – x2020 + x2018 – x2016 + ... + x2 – 1 – ( -x2023 + x2021 – x2019 + x2017 - ... – x3 + x)
= x2022 – x2020 + x2018 – x2016 + ... + x2 – 1 + x2023 – x2021 + x2019 – x2017 + ....+ x3 – x
= ( x2023 + x2022) – (x2021 + x2020) + ....- (x + 1)
Tại x = -1, ta có:
P(-1) = [(-1)2023 + (-1)2022 ] – [ (-1)2021 + (-1)2020] + ....- [(-1) + 1]
=[ (-1) + 1] – [ (-1) + 1) + ... – [(-1) + 1]
= 0 – 0 +....- 0
= 0
Cho 2 đa thức một ẩn có bậc lần lượt là 5 và 3. Đa thức tổng có bậc là
-
A
8
-
B
2
-
C
5
-
D
Không xác định được
Đáp án của giáo viên lời giải hay : C
Viết dạng tổng quát của đa thức bậc 5 và bậc 3 rồi cộng đa thức
Ta có: Đa thức biến x bậc 5 có dạng: a0 + a1. x + a2 . x2 + a3 . x3 + a4 . x4 + a5 . x5 (a5 khác 0)
Đa thức biến x bậc 3 có dạng: b0 + b1. x + b2 . x2 + b3 . x3 (b3 khác 0)
Đa thức tổng của chúng là:
a0 + a1. x + a2 . x2 + a3 . x3 + a4 . x4 + a5 . x5 + b0 + b1. x + b2 . x2 + b3 . x3
= (a0 + b0) + (a1 + b1) . x + (a2 + b2) . x2 + (a3 + b3). x3 + a4 . x4 + a5 . x5
Đa thức này có bậc là 5
Tìm đa thức D(x) thỏa mãn D(x) – (4x2 + 3x3 – x – 3x3 + 4) = x4 – 2x + 2x2 – 1
-
A
- x4 - 2x2 - x - 5
-
B
-x4 - 6x2 + 3x + 3
-
C
x4 - 6x3 + 6x2 – 3x – 5
-
D
x4 + 6x2 – 3x + 3
Đáp án của giáo viên lời giải hay : D
D(x) – A(x) = B(x) thì D(x) = A(x) + B(x). Tính tổng các đa thức
Ta có:
D(x) – (4x2 + 3x3 – x – 3x3 + 4) = x4 – 2x + 2x2 – 1 nên
D(x) = 4x2 + 3x3 – x – 3x3 + 4 + x4 – 2x + 2x2 – 1
= x4 + (3x3 – 3x3 ) + (4x2 + 2x2 ) + (-x – 2x) + (4 – 1)
= x4 + 6x2 – 3x + 3
Cho mảnh đất có kích thước như sau:
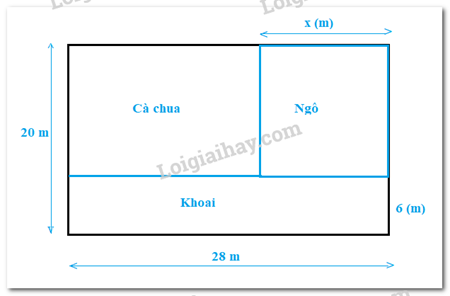
Biết phần đất trồng khoai có dạng hình chữ nhật có kích thước 18 m x 6 m. Biểu diễn diện tích phần đất trồng cà chua theo x
-
A
20.x (m2)
-
B
392 - 14.x (m2)
-
C
560 - 14.x (m2)
-
D
14.x (m2)
Đáp án của giáo viên lời giải hay : B
Diện tích trồng cà chua = Diện tích vườn – diện tích trồng khoai – diện tích trồng ngô
Diện tích hình chữ nhật = chiều dài . chiều rộng
Tổng diện tích ngô và cà chua bằng diện tích của hình chữ nhật có kích thước 28 m x 14 m nên bằng:
28 . 14 = 392 (m2)
Diện tích trồng ngô là: 14 . x (m2)
Diện tích trồng cà chua là:
392 - 14.x (m2)
Biết đa thức A(x) + B(x) = 3x3 – 4x + 4x4 – 6
A(x) – B(x) = 4x3 + 2x - 2x2 + 8 – 2x4
Tìm đa thức A(x)
-
A
2x4 + 7x3 – 2x2 – 2x + 2
-
B
3,5 . x3 – x2 – x + 1
-
C
x4 + \(\frac{7}{2}\)x3 – x2 – x + 1
-
D
- x4 – 0,5 .x3 + x2 + x - 1
Đáp án của giáo viên lời giải hay : C
A = (A + B + A – B) : 2
Ta có:
A(x) +B(x) + A(x) – B(x) = 3x3 – 4x + 4x4 – 6 + 4x3 + 2x - 2x2 + 8 – 2x4
\( \Leftrightarrow \)2. A(x) = (4x4 – 2x4) + (3x3 + 4x3) – 2x2 + (-4x + 2x) + (-6 + 8)
\( \Leftrightarrow \)2. A(x) = 2x4 + 7x3 – 2x2 – 2x + 2
\( \Leftrightarrow \)A(x) = x4 + \(\frac{7}{2}\)x3 – x2 – x + 1
Cho 3 đa thức:
A( x) = 6x2 – 3x + x3 – 4x2 – 5
B(x) = -2x2 – 3x + 7 +2x2 + x3
\(C(x) = 6{x^2} - 3x + 4 - 2{x^3} - 2x\)
Tính A(x) + B(x)
-
A
2x3 + 2x2 – 6x + 2
-
B
2x2 + 2
-
C
4x2 - 6x
-
D
2x3 + 2
Đáp án của giáo viên lời giải hay : A
Bước 1: Thu gọn từng đa thức
Bước 2:
Cách 1: Bỏ dấu ngoặc rồi nhóm các hạng tử cùng bậc.
Cách 2: Đặt tính cộng sao cho các hạng tử cùng bậc đặt thẳng cột với nhau rồi cộng theo từng cột.
Ta có:
A( x) = 6x2 – 3x + x3 – 4x2 – 5 = x3 + (6x2 – 4x2 ) – 3x – 5 = x3 + 2x2 – 3x – 5
B(x) = -2x2 – 3x + 7 +2x2 + x3 = x3 + (-2x2 + 2x2 ) – 3x + 7 = x3 – 3x + 7

Tính A(x) – 3. B(x)
-
A
-2x3 + 2x2 – 12x – 16
-
B
-2x3 + 2x2 + 6x – 16
-
C
4x3 + 2x2 -12x + 21
-
D
2x2 - 2
Đáp án của giáo viên lời giải hay : B
Bước 1: Thu gọn từng đa thức
Bước 2:
Cách 1: Bỏ dấu ngoặc rồi nhóm các hạng tử cùng bậc.
Cách 2: Đặt tính trừ sao cho các hạng tử cùng bậc đặt thẳng cột với nhau rồi trừ theo từng cột.
Ta có:
A( x) = 6x2 – 3x + x3 – 4x2 – 5 = x3 + (6x2 – 4x2 ) – 3x – 5 = x3 + 2x2 – 3x – 5
B(x) = -2x2 – 3x + 7 +2x2 + x3 = x3 + (-2x2 + 2x2 ) – 3x + 7 = x3 – 3x + 7 nên 3. B(x) = 3.(x3 – 3x + 7) = 3x3 – 9x + 21
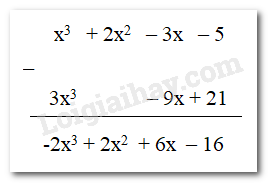
Tìm đa thức \(M\left( x \right)\) biết:
B(x) – M(x) = A(x)
-
A
M(x) = 2x3 + 2x2 – 6x + 2
-
B
M(x) = 2x2 – 2
-
C
M(x) = -2x2 + 2
-
D
M(x) = -2x3 - 2x2 – 6x - 2
Đáp án của giáo viên lời giải hay : C
Bước 1: M(x) = B(x) – A(x)
Bước 2: Thu gọn từng đa thức
Bước 3:
Cách 1: Bỏ dấu ngoặc rồi nhóm các hạng tử cùng bậc.
Cách 2: Đặt tính trừ sao cho các hạng tử cùng bậc đặt thẳng cột với nhau rồi trừ theo từng cột.
Ta có: B(x) – M(x) = A(x) nên M(x) = B(x) – A(x)
A(x) = 6x2 – 3x + x3 – 4x2 – 5 = x3 + (6x2 – 4x2 ) – 3x – 5 = x3 + 2x2 – 3x – 5
B(x) = -2x2 – 3x + 7 +2x2 + x3 = x3 + (-2x2 + 2x2 ) – 3x + 7 = x3 – 3x + 7

Tính A(x) + B(x) – C(x)
-
A
-4x2 – x + 6
-
B
8x2 – 11x – 2
-
C
4x3 + 8x2 + x + 6
-
D
4x3 – 4x2 – x – 2
Đáp án của giáo viên lời giải hay : D
Cách 1: Bỏ dấu ngoặc rồi nhóm các hạng tử cùng bậc.
Cách 2: Đặt tính cộng, trừ sao cho các hạng tử cùng bậc đặt thẳng cột với nhau rồi cộng, trừ theo từng cột.
Ta có:
A(x) = 6x2 – 3x + x3 – 4x2 – 5 = x3 + (6x2 – 4x2 ) – 3x – 5 = x3 + 2x2 – 3x – 5
B(x) = -2x2 – 3x + 7 +2x2 + x3 = x3 + (-2x2 + 2x2 ) – 3x + 7 = x3 – 3x + 7
\(C(x) = 6{x^2} - 3x + 4 - 2{x^3} - 2x\) = -2x3 + 6x2 + (-3x – 2x) + 4 = -2x3 + 6x2 – 5x + 4

