Theo mẫu nguyên tử Bo, trạng thái dừng của nguyên tử:
-
A
Có thể là trạng thái cơ bản hoặc trạng thái kích thích .
-
B
Chỉ là trạng thái kích thích
-
C
Là trạng thái mà các eletron trong nguyên tử ngừng chuyển động.
-
D
Chỉ là trạng thái cơ bản
Đáp án của giáo viên lời giải hay : A
Theo mẫu nguyên tử Bo, trạng thái dừng của nguyên tử có thể là trạng thái cơ bản hoặc trạng thái kích thích.
Theo mẫu nguyên tử Bo, bán kính quỹ đạo dừng được xác định bởi:
-
A
\({r_n} = \frac{{{r_0}}}{{{n^2}}}\)
-
B
\({r_n} = \frac{{{n^2}}}{{{r_0}}}\)
-
C
\({r_n} = {n^2}{r_0}\)
-
D
\({r_n} = {r_0}^{{n^2}}\)
Đáp án của giáo viên lời giải hay : C
Theo mẫu nguyên tử Bo, bán kính quỹ đạo dừng được xác định bởi:
\({r_n} = {n^2}{r_0}\)
Cho bán kính quỹ đạo Bo thứ nhất của nguyên tử H là 0,53.10-10m. Bán kính quỹ đạo Bo thứ 5 của nguyên tử H bằng:
-
A
10,25.10-10m
-
B
2,65.10-10m
-
C
13,25.10-10m
-
D
0,106.10-10m
Đáp án của giáo viên lời giải hay : C
Bán kính của quỹ đạo Bo thứ n là
\({r_n} = {n^2}.{r_0}\)
Bán kính của quỹ đạo Bo thứ 5 là :
\({r_5} = {5^2}.{r_0} = 25.0,{53.10^{ - 10}} = 13,{25.10^{ - 10}}m\)
Trong nguyên tử hiđrô, bán kính Bo là r0 = 5,3.10-11 m. Ở một trạng thái kích thích của nguyên tử hiđrô, êlectron chuyển động trên quỹ đạo dừng có bán kính là r = 13,25.10-10 m. Quỹ đạo đó có tên gọi là quỹ đạo dừng
-
A
N
-
B
M
-
C
O
-
D
P
Đáp án của giáo viên lời giải hay : C
Sử dụng công thức tính bán kính quỹ đạo dừng \({r_n} = {n^2}.{r_0}\)
Quỹ đạo dừng có bán kính rn = 13,25.10-10 m = 52r0 => n = 5 => Quỹ đạo O
Xét nguyên tử hiđrô theo mẫu nguyên tử Bo, trong các quỹ đạo dừng của êlectron có hai quỹ đạo có bán kính rmvà rn. Biết rm− rn= 36r0, trong đó r0 là bán kính Bo. Giá trị rm gần nhất với giá trị nào sau đây?
-
A
100r0
-
B
87r0
-
C
49r0.
-
D
64r0.
Đáp án của giáo viên lời giải hay : A
Áp dụng công thức tính bán kính quỹ đạo ở trạng thái dừng n: rn = n2.r0 kết hợp suy luận toán học
Theo bài ra ta có:
\(\begin{array}{l}{r_m} = {m^2}{r_0}\left( {m \in {N^*}} \right);{r_n} = {n^2}{r_0}\left( {n \in {N^*}} \right)\\ \Rightarrow {r_m} - {r_n} = 36{r_0} \Rightarrow {m^2} - {n^2} = 36 \Rightarrow \left( {m - n} \right)\left( {m + n} \right) = 36\end{array}\)
m – n và m + n là ước của 36. Mặt khác tổng của m – n và m + n là một số chẵn nên hai số m – n và m + n sẽ cùng chẵn hoặc cùng lẻ
\( \Rightarrow \left\{ \begin{array}{l}m - n = 2\\m + n = 18\end{array} \right. \Rightarrow \left\{ \begin{array}{l}m = 10\\n = 8\end{array} \right. \Rightarrow {r_m} = 100{r_0}\)
Nguyên tử Hiđrô đang ở trạng thái dừng có mức năng lượng cơ bản thì hấp thụ một photon có năng lượng \(\varepsilon = {\rm{ }}{E_N}-{\rm{ }}{E_K}\) . Khi đó nguyên tử sẽ:
-
A
Không chuyển lên trạng thái nào cả.
-
B
Chuyển dần từ K lên L rồi lên N.
-
C
Chuyển thẳng từ K lên N.
-
D
Chuyển dần từ K lên L, từ L lên M, từ M lên N.
Đáp án của giáo viên lời giải hay : C
Sử dụng tiên đề về sự bức xạ và hấp thụ năng lượng của nguyên tử: Nếu nguyên tử đang ở trạng thái dừng có năng lượng Em mà hấp thụ được một photon có năng lượng đúng bằng hiệu En – Em thì nó chuyển sang trạng thái dừng có năng lượng En lớn hơn.
Nguyên tử Hiđrô đang ở trạng thái dừng có mức năng lượng cơ bản thì hấp thụ một photon có năng lượng \(\varepsilon = {\rm{ }}{E_N}-{\rm{ }}{E_K}\) .
Khi đó nguyên tử sẽ chuyển thẳng từ K lên N
Trong nguyên tử hiđrô, khi êlêctrôn chuyển động trên quỹ đạo \(K\) với bán kính \(r_0 = 5,3.10^{-11}m\) thì tốc độ của elêctrôn chuyển động trên quỹ đạo đó là:
-
A
2,19.10 6 m / s
-
B
2,19.10 5 m / s
-
C
4,17.10 6 m / s.
-
D
4,17.10 5 m / s
Đáp án của giáo viên lời giải hay : A
Đối với chuyển động của electron trong nguyên tử Hidro, lực Culong đóng vai trò là lực hướng tâm
\({F_C} = {F_{ht}} \Leftrightarrow \dfrac{{k{e^2}}}{{r_n^2}} = \dfrac{{mv_n^2}}{{{r_n}}}\)
\({F_c} = {F_{ht}} \Leftrightarrow \dfrac{{k{e^2}}}{{r_n^2}} = \dfrac{{mv_n^2}}{{{r_n}}} \Rightarrow {v_n} = \sqrt {\dfrac{{k{e^2}}}{{m{r_n}}}} \)
Quỹ đạo K ứng với \(n = 1\)
Ta suy ra tốc độ của electron chuyển động trên quỹ đạo K là: \({v_K} = \sqrt {\dfrac{{{{9.10}^9}.{{\left( {1,{{6.10}^{ - 19}}} \right)}^2}}}{{9,{{1.10}^{ - 31}}.5,{{3.10}^{ - 11}}}}} = 2,{19.10^6}m/s\)
Theo mẫu nguyên tử Bo, êlectron trong nguyên tử hiđrô chuyển động trên các quỹ đạo dừng có bán kính rn = n2r0 (\(n \in N*,\) r0 là bán kính Bo). Tỉ số giữa tốc độ góc của êlectron khi nó chuyển động trên quỹ đạo O và quỹ đạo M là
-
A
\(\dfrac{{\rm{3}}}{{\rm{5}}}\)
-
B
\(\dfrac{9}{{25}}\)
-
C
\(\dfrac{{{\rm{25}}}}{{{\rm{27}}}}\)
-
D
\(\dfrac{{{\rm{27}}}}{{{\rm{125}}}}\)
Đáp án của giáo viên lời giải hay : D
Đối với chuyển động của electron trong nguyên tử Hidro, lực Culong đóng vai trò là lực hướng tâm
\({F_C} = {F_{ht}} = \dfrac{{k{e^2}}}{{r_n^2}} = \dfrac{{mv_n^2}}{{{r_n}}}\)
Sử dụng công thức liên hệ giữa tốc độ dài và tốc độ góc:
\({v_n} = {\omega _n}.{r_n}\)
\({F_{ht}} = \dfrac{{k{e^2}}}{{r_n^2}} = \dfrac{{mv_n^2}}{{{r_n}}} \\\Rightarrow v_n^2 = \dfrac{{k{e^2}}}{{m{r_n}}} = \dfrac{{k{e^2}}}{{m.{n^2}{r_0}}}\)
Lại có:
\({v_n} = {\omega _n}{r_n} = {\omega _n}{n^2}{r_0} \\\Rightarrow {\omega _n} = \dfrac{1}{{{n^3}}}\sqrt {\dfrac{{k{e^2}}}{{mr_0^3}}} \\ \Rightarrow \dfrac{{{\omega _O}}}{{{\omega _M}}} = {\left( {\dfrac{{{n_M}}}{{{n_O}}}} \right)^3} = {\left( {\dfrac{3}{5}} \right)^3} = \dfrac{{27}}{{125}}\)
Trong nguyên tử hidro, tổng của bán kính quỹ đạo thứ \(n\) và bán kính quỹ đạo thứ \(\left( {n + 7} \right)\) bằng bán kính quỹ đạo thứ \(\left( {n + 8} \right)\). Biết bán kính \(r_0=5,3.10^{-11}\). Coi chuyển động của electron quanh hạt nhân là chuyển động tròn đều. Lực tương tác giữa electron và hạt nhân khi electron chuyển động trên quỹ đạo dừng thứ n gần giá trị nào nhất sau đây?
-
A
\(1,{6.10^{ - 10}}N\)
-
B
\(1,{3.10^{ - 10}}N\)
-
C
\(1,{6.10^{ - 11}}N\)
-
D
\(1,{2.10^{ - 11}}N\)
Đáp án của giáo viên lời giải hay : B
+ Sử dụng công thức tính bán kính quỹ đạo \({r_n} = {\text{ }}{n^2}.{r_0}\)
+ Sau đó áp dụng công thức tính lực Cu – lông : \(F = \dfrac{{k{e^2}}}{{{r^2}}}\)
Theo đề bài ta có:
\(\begin{array}{l}{r_n} + {r_{n + 7}} = {r_{n + 8}}\\ \Leftrightarrow {n^2}{r_0} + {(n + 7)^2}{r_0} = {(n + 8)^2}{r_0}\\ \Leftrightarrow {n^2} + {\left( {n + 7} \right)^2} = {\left( {n + 8} \right)^2}\\ \Leftrightarrow {n^2} - 2n - 15 = 0\\ \Rightarrow \left[ \begin{array}{l}n = 5\\n = - 3\left( {loai} \right)\end{array} \right.\end{array}\)
Khi đó lực tương tác giữa electron và hạt nhân trong nguyên tử hidro ở quỹ đạo dừng n là :
\(F = \dfrac{{k{e^2}}}{{{r^2}}} = \dfrac{{{{9.10}^9}.{{(1,{{6.10}^{ - 19}})}^2}}}{{{{(25.5,{{3.10}^{ - 11}})}^2}}} = 1,{3.10^{ - 10}}N\)
Nguyên tử hiđrô được kích thích để chuyển lên quỹ đạo dừng M. Khi nó chuyển về các trạng thái dừng có mức năng lượng thấp hơn thì sẽ phát ra:
-
A
một bức xạ
-
B
hai bức xạ
-
C
ba bức xạ
-
D
bốn bức xạ
Đáp án của giáo viên lời giải hay : C
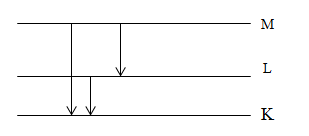
Ba bức xạ ứng với: M về K, L về K, M về L
Xét nguyên tử hidro theo mẫu nguyên tử Bo, các electron chuyển động tròn quanh hạt nhân trên các quỹ đạo dừng dưới tác dụng của lực hút tĩnh điện. Theo định nghĩa dòng điện thì chuyển động của các electron quanh hạt nhân tạo nên dòng điện (gọi là dòng điện nguyên tử, phân tử). Khi electron chuyển động trên quỹ đạo \(L\) thì dòng điện nguyên tử có cường độ \(I_1\) , khi electron chuyển động trên quỹ đạo \(N\) thì dòng điện nguyên tử có cường độ là \(I_2\) . Tỉ số \(\dfrac{I_2}{I_1}\) bằng:
-
A
$\dfrac{1}{8}$
-
B
$\dfrac{1}{4}$
-
C
$8$
-
D
$4$
Đáp án của giáo viên lời giải hay : A
Đối với chuyển động của electron trong nguyên tử Hidro, lực Culong đóng vai trò là lực hướng tâm: \({F_C} = {F_{ht}} \Leftrightarrow k\dfrac{{{e^2}}}{{{r^2}}} = m\dfrac{{{v^2}}}{r}\)
Công thức liên hệ giữa điện tích và cường độ dòng điện: \(I{\rm{ }} = {\rm{ }}q/t\)
Công thức tính bán kính quỹ đạo ở trạng thái dừng n: \({r_n} = {\rm{ }}{n^2}.{r_0}\)
Ta có \(I = \dfrac{q}{t} = \dfrac{q}{T}\xrightarrow{{v = \omega r \Rightarrow T = \dfrac{{2\pi r}}{v}}}I = \dfrac{{|e|v}}{{2\pi r}}\)
Lại có : \(F = k\dfrac{{{e^2}}}{{{r^2}}} = m\dfrac{{{v^2}}}{r} = > v = \sqrt {k\dfrac{{{e^2}}}{{m.r}}} \xrightarrow{{\left( 1 \right)}}I = \dfrac{{|e|\sqrt {k\dfrac{{{e^2}}}{{m.{r^3}}}} }}{{2\pi }} = > \dfrac{{{I_1}}}{{{I_2}}} = \sqrt {{{\left( {\dfrac{{{r_2}}}{{{r_1}}}} \right)}^3}} \)
Khi ở L thì \(n{\text{ }} = {\text{ }}2{\text{ }} = > {\text{ }}{r_1} = {\text{ }}{2^2}.{r_0}\)
Khi ở N thì \(n{\text{ }} = {\text{ }}4{\text{ }}= > {\text{ }}{r_2} = {\text{ }}{4^2}.{r_0}\)
= > \(\dfrac{{{I_1}}}{{{I_2}}} = \sqrt {{{\left( {\dfrac{{{4^2}}}{{{2^2}}}} \right)}^3}} = 8\)
Ta suy ra: \(\dfrac{I_2}{I_1}=\dfrac{1}{8}\)
Khi êlectrôn trong nguyên tử hiđrô chuyển từ quĩ đạo dừng có năng lượng -0,85 eV sang quĩ đạo dừng có năng lượng -13,60 eV thì nguyên tử phát bức xạ điện từ có bước sóng:
-
A
\(0,4340{\rm{ }}\mu m\)
-
B
\(0,4860{\rm{ }}\mu m\)
-
C
\(0,0974{\rm{ }}\mu m\)
-
D
\(0,6563{\rm{ }}\mu m\)
Đáp án của giáo viên lời giải hay : C
Ta có:
\(\Delta E = \frac{{hc}}{\lambda } = - 0,85 - \left( { - 13,6} \right) = 12,75eV \Rightarrow \lambda = \frac{{6,{{625.10}^{ - 34}}{{.3.10}^8}}}{{12,75.1,{{6.10}^{ - 19}}}} = 0,0974\mu m\)
Electron trong nguyên tử Hiđrô chuyển từ quĩ đạo có năng lượng EM = - 1,5eV xuống quỹ đạo có năng lượng EL = - 3,4eV. Tìm bước sóng của vạch quang phổ phát ra?
-
A
Vạch thứ nhất trong dãy Banme, \(\lambda {\rm{ }} = {\rm{ }}0,654{\rm{ }}\mu m{\rm{ }}\;\)
-
B
Vạch thứ hai trong dãy Banme, \(\lambda {\rm{ }} = {\rm{ }}0,654\mu m\)
-
C
Vạch thứ nhất trong dãy Banme, \(\lambda {\rm{ }} = {\rm{ }}0,643\mu m\)
-
D
Vạch thứ ba trong dãy Banme, \(\lambda {\rm{ }} = {\rm{ }}0,458\mu m\)
Đáp án của giáo viên lời giải hay : A
Ta có :
\({E_{M\;}} - \;{E_{L\;}} = \frac{{hc}}{\lambda } = {\rm{ }}1,9.1,{6.10^{ - 19}}J \Rightarrow \lambda = \frac{{6,{{625.10}^{ - 34}}{{.3.10}^8}}}{{1,9.1,{{6.10}^{ - 19}}}} = \;0,654{\rm{ }}\mu m\)
Hai vạch đầu tiên của dãy Laiman trong quang phổ hiđrô có tần số f21 và f31. Từ hai tần số đó người ta tính được tần số đầu tiên f32 trong dãy Banme là:
-
A
f32= f21+ f31
-
B
f32 = f21 - f31
-
C
f32 = f31 – f21
-
D
f32 = (f21 + f31)/2
Đáp án của giáo viên lời giải hay : C
Ta có :
\({E_3} - {E_1} = h{f_{31}};{E_2} - {E_1} = h{f_{21}} \Rightarrow {E_3} - {E_2} = h{f_{32\;}} = \;h{f_{31\;}} - \;h{f_{21}} \Rightarrow \;{f_{32}}\; = {\rm{ }}{f_{31}}\;-{\rm{ }}{f_{21}}\)
Hai vạch đầu tiên của dãy Laiman trong quang phổ hiđrô có bước sóng λ21 và λ31. Từ hai bước sóng đó người ta tính được bước sóng đầu tiên λ32 trong dãy Banme là:
-
A
\({\lambda _{32}}\; = {\rm{ }}\frac{{{\lambda _{31\;}} + \;{\lambda _{21}}}}{2}\)
-
B
\({\lambda _{32}}\; = {\rm{ }}\frac{{{\lambda _{21\;}} - {\rm{ }}{\lambda _{31}}}}{2}\)
-
C
\({\lambda _{32}}\; = \sqrt {\;\left( {{\lambda _{21}}.{\lambda _{31}}} \right)\;\;} \;\)
-
D
\({\lambda _{32}}\; = \;\frac{{{\lambda _{21}}.{\lambda _{31}}}}{{{\lambda _{21\;}} - \;{\lambda _{31}}}}\)
Đáp án của giáo viên lời giải hay : D
Ta có:
\({E_{32}} = {E_3} - {E_2} = \left( {{E_3} - {E_1}} \right) - \left( {{E_2} - {E_1}} \right) \Leftrightarrow \frac{{hc}}{{{\lambda _{32}}}} = \frac{{hc}}{{{\lambda _{31}}}} - \frac{{hc}}{{{\lambda _{21}}}} \Leftrightarrow \frac{1}{{{\lambda _{32}}}} = \frac{1}{{{\lambda _{32}}}} - \frac{1}{{{\lambda _{21}}}} \Rightarrow {\lambda _{32}} = \frac{{{\lambda _{21}}.{\lambda _{32}}}}{{{\lambda _{21}} - {\lambda _{32}}}}\)
Bước sóng của vạch quang phổ thứ nhất và thứ hai của dãy Banme là \(0,656\mu m\) và \(0,486\mu m\) . Bước sóng của vạch đầu tiên trong dãy Pasen là:
-
A
\(0,9672\mu m\)
-
B
\(1,8754\mu m\)
-
C
\(0,7645\mu m\)
-
D
\(1,3627\mu m\)
Đáp án của giáo viên lời giải hay : B
Bước sóng vạch quang phổ thứ nhất của dãy Banme:
\({\lambda _{32}} = {\rm{ }}0,656\mu m\)
Bước sóng vạch quang phổ thứ hai của dãy Banme:
\({\lambda _{42}} = {\rm{ }}0,486\mu m\)
Bước sóng vạch đầu tiên trong trong dãy Pasen:
\({\lambda _{43}}\)
Áp dụng tiên đề Bo:
\(\begin{array}{l}{E_{43}} = {E_4} - {E_3} = {E_4} - {E_2} + {E_2} - {E_3} = \left( {{E_4} - {E_2}} \right) - \left( {{E_3} - {E_2}} \right)\\ \Leftrightarrow \frac{{hc}}{{{\lambda _{43}}}} = \frac{{hc}}{{{\lambda _{42}}}} - \frac{{hc}}{{{\lambda _{32}}}} \Leftrightarrow \frac{1}{{{\lambda _{43}}}} = \frac{1}{{{\lambda _{42}}}} - \frac{1}{{{\lambda _{32}}}} \Rightarrow {\lambda _{43}} = 1,8754\mu m\end{array}\)
Khi chuyển từ quỹ đạo M về quỹ đạo L, nguyên tử hidrô phát ra phôtôn có bước sóng \(0,6563\mu m\) . Khi chuyển từ quỹ đạo N về quỹ đạo L, nguyên tử hidro phát ra phôtôn có bước sóng \(0,4861{\rm{ }}\mu m\) . Khi chuyển từ quỹ đạo N về quỹ đạo M, nguyên tử hidro phát ra phôtôn có bước sóng:
-
A
1,1424µm
-
B
1,8744µm
-
C
0,1702µm
-
D
0,2793µm
Đáp án của giáo viên lời giải hay : B
Khi chuyển từ quỹ đạo M về quỹ đạo L, nguyên tử hidrô phát ra phôtôn có bước sóng:
\({\lambda _{32}} = {\rm{ }}0,6563\mu m\)
Khi chuyển từ quỹ đạo N về quỹ đạo L, nguyên tử hidro phát ra phôtôn có bước sóng :
\({\lambda _{42}} = {\rm{ }}0,4861{\rm{ }}\mu m\)
Khi chuyển từ quỹ đạo N về quỹ đạo M, nguyên tử hidro phát ra phôtôn có bước sóng:
\({\lambda _{43}}\)
Ta có:
\({E_{43}} = {E_4} - {E_3} = \left( {{E_4} - {E_2}} \right) - \left( {{E_3} - {E_2}} \right) \Leftrightarrow \frac{{hc}}{{{\lambda _{43}}}} = \frac{{hc}}{{{\lambda _{42}}}} - \frac{{hc}}{{{\lambda _{32}}}} \Leftrightarrow \frac{1}{{{\lambda _{43}}}} = \frac{1}{{{\lambda _{42}}}} - \frac{1}{{{\lambda _{32}}}} \Rightarrow {\lambda _{43}} = \frac{{{\lambda _{32}}{\lambda _{42}}}}{{{\lambda _{32}} - {\lambda _{42}}}} = 1,8744\mu m\)
Khi êlectron ở quỹ đạo dừng thứ n thì năng lượng của nguyên tử hiđrô được tính theo công thức \({E_n} = - \frac{{{E_0}}}{{{n^2}}}\) (eV) (E0 là một hằng số dương và n = 1,2,3. . .). Khi êlectron trong nguyên tử hiđrô chuyển từ quỹ đạo dừng thứ n + 1 sang quỹ đạo dừng thứ n thì nguyên tử hiđrô phát ra phôtôn có bước sóng \({\lambda _0}\) có năng lượng \(\frac{{5{E_0}}}{{36}}\) (eV). Khi êlectron chuyển từ quỹ đạo L về quỹ đạo K thì nguyên tử phát ra phôtôn có bước sóng là
-
A
\(\frac{{5{\lambda _0}}}{{27}}\)
-
B
\(\frac{{7{\lambda _0}}}{{18}}\)
-
C
\(\frac{{5{\lambda _0}}}{{32}}\)
-
D
\(\frac{{7{\lambda _0}}}{9}\)
Đáp án của giáo viên lời giải hay : A
Khi e chuyển từ quỹ đạo L về quỹ đạo K thì phát phát ra photon có năng lượng:
\(\Delta E = \left( { - \frac{1}{{{2^2}}} - \left( { - \frac{1}{{{1^2}}}} \right)} \right){E_0} = \frac{{3{E_0}}}{4}\left( {eV} \right) = \frac{{hc}}{\lambda }(1)\)
Khi êlectron trong nguyên tử hiđrô chuyển từ quỹ đạo dừng thứ n + 1 sang quỹ đạo dừng thứ n:
\(\Delta E' = \frac{{5{E_0}}}{{36}} = \frac{{hc}}{{{\lambda _0}}}(2)\)
(1) : (2) ta được:
\(\lambda = \frac{5}{{27}}{\lambda _0}\)
Trong quang phổ của nguyên tử hiđrô, giả sử f1, f2 tương ứng với tần số lớn nhất và nhỏ nhất của dãy Ban-me, f3 là tần số lớn nhất của dãy Pa-sen thì
-
A
\({f_1} = {\rm{ }}{f_2}-{\rm{ }}{f_3}\)
-
B
\({f_3} = \dfrac{{{f_{\rm{1}}} + {f_{\rm{2}}}}}{{\rm{2}}}\)
-
C
\({f_1} = {\rm{ }}{f_2} + {\rm{ }}{f_3}\) .
-
D
\({f_3} = {\rm{ }}{f_1} + {\rm{ }}{f_2}\) .
Đáp án của giáo viên lời giải hay : C
Áp dụng tiên đề Bo về sự bức xạ và hấp thụ năng lượng của nguyên tử
\({E_{mn}} = {\rm{ }}{E_m} - {\rm{ }}{E_n} = \dfrac{{hc}}{\lambda } = hf\)
Từ giản đồ năng lượng của Hiđrô ta có:
\({f_1} = {\rm{ }}{f_{\infty 2}};{\rm{ }}{f_2} = {\rm{ }}{f_{32}};{\rm{ }}{f_3} = {\rm{ }}{f_{\infty 3}}\)
Áp dụng tiên đề Bo:
\(\begin{array}{l}h{f_\infty }_3 = {\rm{ }}{E_\infty } - {\rm{ }}{E_3} = {\rm{ }}{E_\infty } - {\rm{ }}{E_2} + {\rm{ }}{E_2} - {\rm{ }}{E_3}\;\\ \Leftrightarrow h{f_\infty }_3 = h{f_\infty }_2 + h{f_{23}} \\\Leftrightarrow {f_\infty }_3 = {f_\infty }_2 + {f_{23}} = {f_\infty }_2 - {f_{32}} \\\Leftrightarrow {f_3} = {f_1} - {f_2} \\\Leftrightarrow {f_1} = {f_2} + {f_3}\end{array}\)
Bước sóng của hai vạch \({H_\alpha }\) và \({H_\beta }\) trong dãy Banme là \({\lambda _1} = {\rm{ }}656nm\) và \({\lambda _2}\; = {\rm{ }}486nm\) . Bước sóng của vạch quang phổ đầu tiên trong dãy Pasen
-
A
\(1,8754\mu m\)
-
B
\(0,18754\mu m\)
-
C
\(18,754\mu m\)
-
D
\(187,54\mu m\)
Đáp án của giáo viên lời giải hay : A
Áp dụng tiên đề Bo về sự bức xạ và hấp thụ năng lượng của nguyên tử \({E_{mn}} = {\rm{ }}{E_m} - {\rm{ }}{E_n} = \frac{{hc}}{\lambda }\)
Bước sóng của vạch H:
\({\lambda _{32}} = {\rm{ }}{\lambda _1} = 656nm\)
Bước sóng của vạch H:
\({\lambda _{42}} = {\rm{ }}{\lambda _2} = 486nm\)
Bước sóng của vạch quang phổ đầu tiên trong dãy Pasen:
\({\lambda _{43}}\)
\(\frac{1}{{{\lambda _{43}}}} = \frac{1}{{{\lambda _{42}}}} - \frac{1}{{{\lambda _{32}}}} = \frac{1}{{{\lambda _2}}} - \frac{1}{{{\lambda _1}}} \Rightarrow {\lambda _{43}} = \frac{{{\lambda _1}{\lambda _2}}}{{{\lambda _1} - {\lambda _2}}} = 1875,4nm = 1,8754\mu m\)
Trong quang phổ hidro, bước sóng dài nhất của dãy Laiman là \(0,1216\mu m\) , bước sóng ngắn nhất của dãy Banme là \(0,3650{\rm{ }}\mu m\) . Bước sóng ngắn nhất của bức xạ mà hiđrô có thể phát ra:
-
A
0,4866 µm
-
B
0,2434 µm
-
C
0,6563 µm
-
D
0,0912 µm
Đáp án của giáo viên lời giải hay : D
Áp dụng tiên đề Bo về sự bức xạ và hấp thụ năng lượng của nguyên tử
\({E_{mn}} = {\rm{ }}{E_m} - {\rm{ }}{E_n} = \frac{{hc}}{\lambda }\)
Ta có:
\(\Delta E = \frac{{hc}}{\lambda } \to \lambda \)lớn nhất khi E nhỏ nhất, \(\lambda \) nhỏ nhất khi \(\Delta E\) lớn nhất
Bước sóng dài nhất của dãy Laiman là:
\({\lambda _{21}} = \;0,1216\mu m\)
Bước sóng ngắn nhất của dãy Banme là:
\({\lambda _{\infty 2}}\; = 0,3650{\rm{ }}\mu m\)
Bước sóng ngắn nhất của bức xạ mà hiđrô có thể phát ra:
\({\lambda _{\infty 1}}\)
\(\frac{1}{{{\lambda _{\infty 1}}}} = \frac{1}{{{\lambda _{\infty 2}}}} + \frac{1}{{{\lambda _{21}}}} \Rightarrow {\lambda _{\infty 1}} = \frac{{{\lambda _{\infty 2}}{\lambda _{21}}}}{{{\lambda _{\infty 2}} + {\lambda _{21}}}} = 0,0912\mu m\)
Trong nguyên tử hiđrô các mức năng lượng được mô tả theo công thức E = -A/n2, trong đó A là hằng số dương. Khi nguyên tử đang ở trạng thái cơ bản thì bị kích thích bởi điện trường mạnh và làm cho nguyên tử có thể phát ra tối đa 15 bức xạ. Hỏi trong các bức xạ mà nguyên tử hiđrô có thể phát ra trong trường hợp này thì tỉ số về bước sóng giữa bức xạ dài nhất và ngắn nhất là bao nhiêu?
-
A
79,5
-
B
900/11
-
C
1,29
-
D
6
Đáp án của giáo viên lời giải hay : A
Áp dụng tiên đề Bo về sự bức xạ và hấp thụ năng lượng của nguyên tử và công thức tính số bức xạ nguyên tử có thể phát ra: n.(n – 1)/2
Do nguyên tử có thể phát ra tối đa 15 bức xạ n.(n – 1)/2 = 15 n = 6
Ta có:
\(\Delta E = \frac{{hc}}{\lambda } \to \lambda \)lớn nhất khi E nhỏ nhất, \(\lambda \) nhỏ nhất khi E lớn nhất
Bước sóng dài nhất:
\({\lambda _{max}} = {\lambda _{65}}\)
Bước sóng nhỏ nhất:
\({\lambda _{min}} = {\lambda _{61}}\)
\(\left\{ \begin{array}{l}\frac{{hc}}{{{\lambda _{m{\rm{ax}}}}}} = \frac{{hc}}{{{\lambda _{65}}}} = {E_6} - {E_5} = A\left( {\frac{1}{{25}} - \frac{1}{{36}}} \right)\\\frac{{hc}}{{{\lambda _{\min }}}} = \frac{{hc}}{{{\lambda _{61}}}} = {E_6} - {E_1} = A\left( {1 - \frac{1}{{36}}} \right)\end{array} \right. \Rightarrow \frac{{{\lambda _{m{\rm{ax}}}}}}{{{\lambda _{\min }}}} = 79,5\)
Một nguyên tử chuyển từ trạng thái dừng Em sang trạng thái dừng En (Em < En) khi hấp thụ một photon có năng lượng hf. Chọn câu đúng:
-
A
\(hf = {E_n} - {E_m}\)
-
B
\(hf \ge {E_n} - {E_m}\)
-
C
\(hf \leqslant {E_n} - {E_m}\)
-
D
\(hf > {E_n} - {E_m}\)
Đáp án của giáo viên lời giải hay : A
Ta có: Khi nguyên tử chuyển từ trạng thái dừng có năng lượng En sang trạng thái có năng lượng Em < En thì nó phát ra một photon có năng lượng $\varepsilon = {E_n} - {E_m}$.
Chọn câu sai về hai tiên đề của Bo:
-
A
Trạng thái dừng là trạng thái có năng lượng xác định mà nguyên tử tồn tại mà không bức xạ.
-
B
Trạng thái dừng có mức năng lượng càng thấp thì càng bền vững.
-
C
Nguyên tử phát ra một phôtôn khi chuyển từ trạng thái dừng có mức năng lượng thấp Em sang trạng thái dừng có mức năng lượng cao hơn En.
-
D
Năng lượng của phôtôn hấp thụ hay phát ra bằng đúng với hiệu hai mức năng lượng mà nguyên tử dịch chuyển: \(\varepsilon = {E_n} - {E_m}\) (với En > Em).
Đáp án của giáo viên lời giải hay : C
A, B, D - đúng
C - sai vì: khi chuyển từ trạng thái dừng có mức năng lượng thấp Em sang trạng thái dừng có mức năng lượng cao hơn En thì nguyên tử hấp thụ photon
Khối khí hidro có các nguyên tử đang ở trạng thái kích thích thứ nhất thì khối khí nhận thêm năng lượng và chuyển lên trạng thái kích thích mới. Biết rằng ở trạng thái kích thích mới, electron chuyển động trên quỹ đạo có bán kính gấp 49 lần bán kính Bo thứ nhất. Số các bức xạ có tần số khác nhau tối đa mà khối khí hidro có thể phát ra là
-
A
15
-
B
30
-
C
21
-
D
42
Đáp án của giáo viên lời giải hay : C
+ Sử dụng biểu thức: \({r_n} = {n^2}{r_0}\)
+ Sử dụng biểu thức xác định số bức xạ phát ra: \(\dfrac{{n\left( {n - 1} \right)}}{2}\)
Ta có: \({r_n} = {n^2}{r_0} = 49{r_0} \Rightarrow n = 7\)
Số bức xạ có tần số khác nhau tối đa mà khối khí hidro có thể phát ra là: \(\dfrac{{n\left( {n - 1} \right)}}{2} = \dfrac{{7.6}}{2} = 21\)
Một đám nguyên tử hiđrô đang ở trạng thái cơ bản. Khi chiếu bức xạ có tần số f1 vào đám nguyên tử này thì chúng phát ra tối đa 3 bức xạ. Khi chiếu bức xạ có tần số f2 vào đám nguyên tử này thì chúng phát ra tối đa 10 bức xạ. Biết năng lượng ứng với các trạng thái dừng của nguyên tử hiđrô được tính theo biểu thức \({{\rm{E}}_{\rm{n}}} = - \dfrac{{{{\rm{E}}_0}}}{{{{\rm{n}}^2}}}\) (E0 là hằng số dương, n = 1,2,3,…). Tỉ số \(\dfrac{{{{\rm{f}}_1}}}{{{{\rm{f}}_2}}}\) là
-
A
\(\dfrac{{10}}{3}\).
-
B
\(\dfrac{{27}}{{25}}\).
-
C
\(\dfrac{3}{{10}}\).
-
D
\(\dfrac{{25}}{{27}}\) .
Đáp án của giáo viên lời giải hay : D
Số bức xạ phát ra: \(N = \dfrac{{n\left( {n - 1} \right)}}{2}\)
Năng lượng của photon: \(\varepsilon = hf = \dfrac{{hc}}{\lambda } = {E_{cao}} - {E_{thap}}\) với \({E_n} = - \dfrac{{{E_0}}}{{{n^2}}}\)
Với tần số \({f_1}\), số bức xạ phát ra là: \(\dfrac{{{n_1}\left( {{n_1} - 1} \right)}}{2} = 3 \Rightarrow {n_1} = 3\)
Với tần số \({f_2}\), số bức xạ phát ra là: \(\dfrac{{{n_2}\left( {{n_2} - 1} \right)}}{2} = 10 \Rightarrow {n_2} = 5\)
Ta có:
\(\left\{ \begin{array}{l}h{f_1} = {E_3} - {E_1}\\h{f_2} = {E_5} - {E_1}\end{array} \right. \Rightarrow \dfrac{{{f_1}}}{{{f_2}}} = \dfrac{{{E_3} - {E_1}}}{{{E_5} - {E_1}}} = \dfrac{{\dfrac{{ - {E_0}}}{9} - \left( {\dfrac{{ - {E_0}}}{1}} \right)}}{{\dfrac{{ - {E_0}}}{{25}} - \left( {\dfrac{{ - {E_0}}}{1}} \right)}} = \dfrac{{\dfrac{{ - 1}}{9} + 1}}{{\dfrac{{ - 1}}{{25}} + 1}} = \dfrac{{25}}{{27}}\)
Theo các tiên đề Bo, trong nguyên tử Hiđrô, giả sử chuyển động của electron quanh hạt nhân là chuyển động tròn đều. Tỉ số giữa tốc độ của electron trên quỹ đạo K với tốc độ của electron trên quỹ đạo N bằng
-
A
4
-
B
3
-
C
6
-
D
9
Đáp án của giáo viên lời giải hay : A
Lực tĩnh điện đóng vai trò là lực hướng tâm:
\(k\dfrac{{{e^2}}}{{r_n^2}} = \dfrac{{mv_n^2}}{{{r_n}}} \Rightarrow {v_n} = \sqrt {\dfrac{{k.{e^2}}}{{m.{r_n}}}} = \sqrt {\dfrac{{k.{e^2}}}{{m.{n^2}.{r_0}}}} \)
Ta có: \(\left\{ \begin{array}{l}k\dfrac{{{e^2}}}{{r_n^2}} = \dfrac{{mv_n^2}}{{{r_n}}}\\{r_n} = {n^2}.{r_0}\end{array} \right. \Rightarrow {v_n} = \sqrt {\dfrac{{k.{e^2}}}{{m.{r_n}}}} = \sqrt {\dfrac{{k.{e^2}}}{{m.{n^2}.{r_0}}}} \)
Mức K ứng với n = 1; Mức N ứng với n = 4
Tỉ số giữa tốc độ của electron trên quỹ đạo K với tốc độ của electron trên quỹ đạo N:
\(\dfrac{{{v_K}}}{{{v_N}}} = \sqrt {\dfrac{{{r_N}}}{{{r_K}}}} = \sqrt {\dfrac{{{4^2}.{r_0}}}{{1.{r_0}}}} = 4\)
Các mức năng lượng của các trạng thái dừng của nguyên tử hidro được xác định bằng biểu thức \({{E}_{n}}=-\frac{13,6}{{{n}^{2}}}eV\,\,\left( n=1,2,3,... \right)\). Nếu nguyên tử hidro hấp thụ một photon có năng lượng 2,55eV thì bước sóng nhỏ nhất của bức xạ mà nguyên tử hidro có thể phát ra là
-
A
\(9,{{74.10}^{-8}}m\).
-
B
\(1,{{46.10}^{-8}}m\).
-
C
\(1,{{22.10}^{-8}}m\).
-
D
\(4,{{87.10}^{-8}}m\).
Đáp án của giáo viên lời giải hay : A
Tiên đề về sự bức xạ và hấp thụ năng lượng của nguyên tử:
+ Khi nguyên tử chuyển từ trạng thái dừng có năng lượng (En) sang trạng thái dừng có năng lượng thấp hơn (Em) thì nó phát ra một photon có năng lượng đúng bằng hiệu En – Em:
\(\varepsilon =\frac{hc}{{{\lambda }_{nm}}}={{E}_{n}}-{{E}_{m}}\)
+ Ngược lại, nếu nguyên tử đang ở trạng thái dừng có năng lượng Em mà hấp thụ được một photon có năng lượng đúng bằng hiệu En – Em thì nó chuyển lên trạng thái dừng có năng lượng cao En.
Ta có
\({{E}_{n}}=-\frac{13,6}{{{n}^{2}}}eV\Rightarrow \left\{ \begin{align}& {{E}_{1~}}=-13,6eV \\& {{E}_{2~}}=-3,4eV \\& {{E}_{3~}}=-1,51eV \\& {{E}_{4~}}=-0,85eV \\\end{align} \right.\)
Thấy rằng : \({{E}_{4}}~-{{E}_{2}}~=-0,85+3,44=2,55eV\)
→ Nguyên tử hidro hấp thụ năng lượng 2,55 eV và nhảy từ mức n = 2 lên mức n = 4.
Nguyên tử Hidro có thể phát ra bước sóng nhỏ nhất khi nó chuyển từ mức 4 xuống mức 1. Ta có:
\(\begin{align}& {{E}_{4}}-{{E}_{1}}=\frac{hc}{{{\lambda }_{41}}}\Rightarrow {{\lambda }_{41}}=\frac{hc}{{{E}_{4}}-{{E}_{1}}} \\& \Rightarrow {{\lambda }_{41}}=\frac{6,{{625.10}^{-34}}{{.3.10}^{8}}}{\left( -0,85+13,6 \right).1,{{6.10}^{-19}}}=9,{{74.10}^{-8}}m \\\end{align}\)
Theo tiên đề Bo, bán kính Bo là r0 = 5,3.10-11m. Coi rằng ở trạng thái dừng thứ n của nguyên tử, electron chuyển động tròn đều xung quanh hạt nhân với bán kính quỹ đạo dừng tương ứng là rn = n2.r0 (n = 1,2,3,…). Khi electron của nguyên tử chuyển động trên quỹ đạo dừng có bán kính 132,5.10-11 m thì trong thời gian ∆t electron đi được quãng đường 3S. Cũng trong khoảng thời gian ∆t, nếu electron chuyển động trên quỹ đạo dừng có bán kính r (ứng với tên quỹ đạo là M) sẽ đi được quãng đường là
-
A
4S.
-
B
5,3S
-
C
5S
-
D
1,5S
Đáp án của giáo viên lời giải hay : C
Lực Cu-long đóng vai trò lực hướng tâm.
Ta xác định vận tốc của electron trên các quỹ đạo tương ứng.
Quãng đường đi được của electron trong thời gian ∆t là S = v.∆t.
Sử dụng bảng số thứ tự và tên quỹ đạo
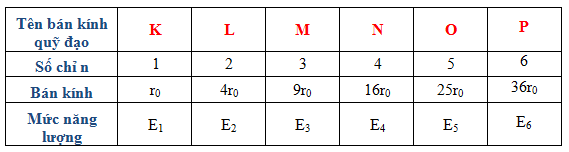
Ta có:
\(r = 132,{5.10^{ - 11}}m = {5^2}.{r_0} \Rightarrow n = 5\)→ Quỹ đạo dừng O
Quỹ đạo dừng M ứng với n = 3.
Lực Cu-long đóng vai trò lực hướng tâm, ta có:
\(k.\frac{{{e^2}}}{{r_n^2}} = m.\frac{{{v^2}}}{{{r_n}}} \Rightarrow v = \sqrt {\frac{{k.{e^2}}}{{m.{r_n}}}} = \frac{1}{n}.\sqrt {\frac{{k.{e^2}}}{{m.{r_0}}}} \)
Trên các quỹ đạo O và M tương ứng là các vận tốc vO và vM. ta có tỉ số:
\(\frac{{{v_O}}}{{{v_M}}} = \frac{{{n_M}}}{{{n_O}}} = \frac{3}{5} \Rightarrow {v_M} = \frac{5}{3}{v_O}\)
Quãng đường đi được của electron trong thời gian ∆t trên mỗi quỹ đạo O và M tương ứng là:
\(\left\{ \begin{array}{l}
{S_O} = 3S = {v_O}.\Delta t\\
{S_M} = {v_M}.\Delta t = \frac{5}{3}.{v_O}.\Delta t = \frac{5}{3}.3S = 5S
\end{array} \right.\)
Kích thích cho các nguyên tử hiđrô chuyển từ trạng thái cơ bản lên trạng thái kích thích sao cho bán kính quỹ đạo dừng tăng 25 lần. Trong quang phổ phát xạ của nguyên tử hiđrô sau đó, tỉ số giữa bước sóng ngắn nhất và bước sóng dài nhất là
-
A
\(\frac{{348}}{9}\)
-
B
\(\frac{9}{{384}}\)
-
C
\(\frac{9}{{348}}\)
-
D
\(\frac{{384}}{9}\)
Đáp án của giáo viên lời giải hay : B
Công thức tính bán kính quỹ đạo của electron trong các trạng thái dừng là:
\({r_n} = {n^2}.{r_0};\,\,n = 1,2,3, \ldots \)
Khi nguyên tử chuyển từ mức năng lượng cao về mức năng lượng thấp hơn thì nó phát ra một photon có năng lượng bằng hiệu hai mức:
\(\varepsilon = \frac{{hc}}{\lambda } = {E_m} - {E_n}\)
Năng lượng của các trạng thái dừng là:
\({E_n} = \frac{{{E_0}}}{{{n^2}}}\)
Công thức tính bán kính quỹ đạo của electron trong các trạng thái dừng là:
\({r_n} = {n^2}.{r_0};\,\,n = 1,2,3, \ldots \)
Nguyên tử ở trạng thái mà bán kính quỹ đạo là:
\(\;{r_n} = 25{r_0} \Leftrightarrow {n^2}{r_0} = 25{r_0} \Rightarrow n = 5\)
Tức là nguyên tử đang ở mức O
Khi nguyên tử chuyển từ mức năng lượng cao về mức năng lượng thấp hơn thì nó phát ra một photon có năng lượng bằng hiệu hai mức:
\(\varepsilon = \frac{{hc}}{\lambda } = {E_m} - {E_n}\)
Bức xạ có bước sóng dài nhất ứng với chuyển từ mức O về mức N (n = 4):
\({\varepsilon _1} = \frac{{hc}}{{{\lambda _{\max }}}} = {E_O} - {E_N} = \frac{{{E_0}}}{{{5^2}}} - \frac{{{E_0}}}{{{4^2}}}\)
Bức xạ có bước sóng ngắn nhất ứng với chuyển từ mức O về mức K (n = 1) :
\({\varepsilon _2} = \frac{{hc}}{{{\lambda _{\min }}}} = {E_O} - {E_K} = \frac{{{E_0}}}{{{5^2}}} - \frac{{{E_0}}}{{{1^2}}}\)
Tỉ số giữa bước sóng ngắn nhất và bước sóng dài nhất là :
\(\frac{{{\lambda _{\min }}}}{{{\lambda _{\max }}}} = \frac{{{\varepsilon _1}}}{{{\varepsilon _2}}} = \frac{{\frac{{{E_0}}}{{{5^2}}} - \frac{{{E_0}}}{{{4^2}}}}}{{\frac{{{E_0}}}{{{5^2}}} - {E_0}}} = \frac{{\frac{1}{{{5^2}}} - \frac{1}{{{4^2}}}}}{{\frac{1}{{{5^2}}} - 1}} = \frac{3}{{128}} = \frac{9}{{384}}\)
Xét nguyên tử hiđrô theo mẫu nguyên tử Bo. Quỹ đạo dừng N của êlectron trong nguyên tử ứng với số nguyên n bằng
-
A
3
-
B
2.
-
C
5.
-
D
4.
Đáp án của giáo viên lời giải hay : D
Sử dụng bảng quy đổi tên bán kính quỹ đạo dừng:

Quỹ đạo dừng N của electron trong nguyên tử ứng với n = 4.
Trong nguyên tử hiđrô, bán kính Bo là \(5,{3.10^{ - 11}}m\). Khi ở trạng thái kích thích, êlectron chuyển động trên quỹ đạo dừng L có bán kính là
-
A
\(6,{48.10^{ - 10}}m\)
-
B
\(4,{77.10^{ - 10}}m\)
-
C
\(1,{06.10^{ - 10}}m\)
-
D
\(2,{12.10^{ - 10}}m\)
Đáp án của giáo viên lời giải hay : D
+ Sử dụng bảng quy đổi tên bán kính quỹ đạo dừng:

+ Công thức tính bán kính quỹ đạo dừng n: \({r_n} = {n^2}{r_0}\)
Quỹ đạo L ứng với \(n = 2\)
\( \Rightarrow \) Bán kính quỹ đạo L:
\({r_L} = {2^2}{r_0} = 4.5,{3.10^{ - 11}} = 2,{12.10^{ - 10}}m\)
Trong quang phổ của nguyên tử hiđrô, các vạch phổ nhìn thấy được có màu đỏ, chàm, tím và màu nào sau đây?
-
A
Cam
-
B
Lam
-
C
Lục
-
D
Vàng
Đáp án của giáo viên lời giải hay : B
Sử dụng lý thuyết quang phổ vạch của nguyên tử hiđrô.
Trong quang phổ của nguyên tử hiđrô, các vạch phổ nhìn thấy được gồm: đỏ, lam, chàm, tím.
