Chọn câu sai.
-
A
Trong một tam giác có ba đường trung tuyến
-
B
Các đường trung tuyến của tam giác cắt nhau tại một điểm.
-
C
Giao của ba đường trung tuyến của một tam giác gọi là trọng tâm của tam giác đó.
-
D
Một tam giác có ba trọng tâm
Đáp án của giáo viên lời giải hay : D
Sử dụng kiến thức về ba đường trung tuyến.
“ Ba đường trung tuyến của một tam giác cùng đi qua một điểm. Điểm gặp nhau của ba đường trung tuyến gọi là trọng tâm của tam giác đó.”
+ Một tam giác chỉ có một trọng tâm nên đáp án D sai.
Tam giác \(ABC\) có trung tuyến \(AM = 12\,cm\) và trọng tâm \(G\). Độ dài đoạn \(AG\) là
-
A
\(4,5\,cm\)
-
B
\(3\,cm\)
-
C
\(6\,cm\)
-
D
\(8\,cm\)
Đáp án của giáo viên lời giải hay : D
Trọng tâm cách đỉnh một khoảng bằng \(\dfrac{2}{3}\) đường trung tuyến kẻ từ đỉnh đó.
Vì \(G\) là trọng tâm tam giác \(ABC\) và \(AM\) là đường trung tuyến nên \(AG = \dfrac{2}{3}AM\) (tính chất ba đường trung tuyến của tam giác)
Do đó $AG = \dfrac{2}{3}.12 = 8\,cm.$
Cho \(G\) là trọng tâm của tam giác đều. Chọn câu đúng.
-
A
\(GA = GB = GC\)
-
B
\(GA = GB > GC\)
-
C
\(GA < GB < GC\)
-
D
\(GA > GB > GC\)
Đáp án của giáo viên lời giải hay : A
- Xét các tam giác bằng nhau, suy ra các cạnh tương ứng bằng nhau.
- Áp dụng tính chất đường trung tuyến của tam giác.
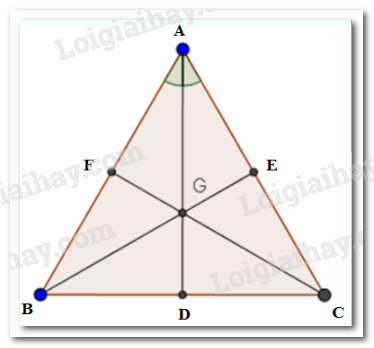
Các tia $AG,BG$ và $CG$ cắt $BC,AC,AB$ lần lượt tại $D,E,F$ thì $D,E,F$ theo thứ tự là trung điểm của $BC,AC,AB.$
Mà $BC = AC = AB$ (do tam giác $ABC$ là tam giác đều), do đó $BD = DC = CE = EA = AF = FB$
Xét \(\Delta AEB\) và \(\Delta AFC\) ta có: $AB = AC;$ \(\widehat A\) chung; $AE = AF.$
Vậy \(\Delta AEB = AFC\,(c.g.c)\), suy ra $BE = CF\,\,\,\,\left( 1 \right)$
Chứng minh tương tự ta có \(\Delta BEC = ADC\,(c.g.c)\), suy ra $BE = AD\left( 2 \right)$
Từ (1) và (2) ta có: $AD = BE = CF\left( 3 \right)$
Theo đề bài $G$ là trọng tâm của tam giác $ABC$ nên ta có:
\(GA = \dfrac{2}{3}AD;\,\,GB = \dfrac{2}{3}BE;\,\,GC = \dfrac{2}{3}CF\)
Vì thế từ (3) ta suy ra $GA = GB = GC.$
Cho tam giác \(ABC\) có hai đường trung tuyến \(BD;CE\) sao cho \(BD = CE\). Khi đó tam giác \(ABC\)
-
A
Cân tại \(B.\)
-
B
Cân tại \(C.\)
-
C
Vuông tại \(A.\)
-
D
Cân tại \(A.\)
Đáp án của giáo viên lời giải hay : D
+ Sử dụng tính chất về đường trung tuyến của tam giác
+ Chứng minh hai tam giác bằng nhau \(\Delta BGE = \Delta CGD\left( {c - g - c} \right)\)
+ Từ đó suy ra tính chất của tam giác \(ABC.\)
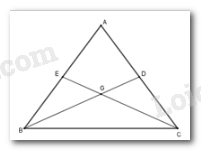
Hai đường trung tuyến \(BD;CE\) cắt nhau tại \(G\) nên \(G\) là trọng tâm tam giác \(ABC.\)
\(\Rightarrow\) \(BG = \dfrac{2}{3}BD;\,CG = \dfrac{2}{3}CE\) mà \(BD = CE \Rightarrow \)\(BG = CG.\)
Ta được: \(BD - BG = CE - CG \Rightarrow GD = GE\)
Xét \(\Delta BGE\) và \(\Delta CGD\) có
+ \(BG = CG\)
+ \(\widehat {BGE} = \widehat {CGD}\) (đối đỉnh)
+ \(GD = GE\)
Nên \(\Delta BGE = \Delta CGD\left( {c - g - c} \right)\)
\(\Rightarrow\) \(BE = CD \Rightarrow \dfrac{1}{2}AB = \dfrac{1}{2}AC\) do đó \(AB = AC\) hay tam giác $ABC$ cân tại \(A.\)
Cho tam giác \(ABC\), các đường trung tuyến \(BD\) và \(CE\). Chọn câu đúng.
-
A
\(BD + CE < \dfrac{3}{2}BC\)
-
B
\(BD + CE > \dfrac{3}{2}BC\)
-
C
\(BD + CE = \dfrac{3}{2}BC\)
-
D
\(BD + CE = BC\)
Đáp án của giáo viên lời giải hay : B
+ Sử dụng tính chất đường trung tuyến của tam giác và quan hệ giữa các cạnh trong tam giác
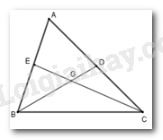
Gọi \(G\) là giao điểm của \(BD\) và \(CE\). Trong \(\Delta GBC\) ta có \(BG + CG > BC\)
Ta lại có \(BG = \dfrac{2}{3}BD;\,CG = \dfrac{2}{3}CE\) (tính chất các đường trung tuyến của tam giác \(ABC\))
Từ đó \(\dfrac{2}{3}BD + \dfrac{2}{3}CE > BG + CG\)\( \Rightarrow \dfrac{2}{3}\left( {BD + CE} \right) > BC\)\( \Rightarrow BD + CE > \dfrac{3}{2}BC.\)
Cho tam giác \(ABC\), đường trung tuyến \(BD\). Trên tia đối của tia $DB$ lấy điểm \(E\) sao cho \(DE = DB.\) Gọi \(M,N\) theo thứ tự là trung điểm của \(BC;CE.\) Gọi \(I;K\) theo thứ tự là giao điểm của \(AM,AN\) với \(BE.\) Chọn câu đúng.
-
A
\(BI = IK > KE\)
-
B
\(BI > IK > KE\)
-
C
\(BI = IK = KE\)
-
D
\(BI < IK < KE\)
Đáp án của giáo viên lời giải hay : C
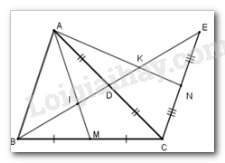
\(I\) là trọng tâm tam giác \(ABC\) nên \(BI = \dfrac{2}{3}BD = \dfrac{1}{3}BE\) \(\left( 1 \right)\)
\(K\) là trọng tâm tam giác \(ACE\) nên \(EK = \dfrac{2}{3}ED = \dfrac{1}{3}BE\,\,\,\left( 2 \right)\)
Từ \(\left( 1 \right);\left( 2 \right)\) suy ra \(IK = \dfrac{1}{3}BE\) từ đó \(BI = EK = IK\) .
Cho tam giác \(ABC\) có hai đường phân giác \(CD\) và \(BE\) cắt nhau tại \(I.\) Khi đó
-
A
\(AI\) là trung tuyến vẽ từ \(A.\)
-
B
\(AI\) là đường cao kẻ từ \(A.\)
-
C
\(AI\) là trung trực cạnh \(BC.\)
-
D
\(AI\) là phân giác của góc \(A.\)
Đáp án của giáo viên lời giải hay : D
Ba đường phân giác của tam giác cùng đi qua 1 điểm.
Hai đường phân giác \(CD\) và \(BE\) cắt nhau tại \(I\) mà ba đường phân giác của một tam giác cùng đi qua một điểm nên \(AI\) là phân giác của góc \(A.\)
Cho \(\Delta ABC\), các tia phân giác của góc $B$ và $A$ cắt nhau tại điểm $O.$ Qua $O$ kẻ đường thẳng song song với $BC$ cắt $AB$ tại $M,$ cắt $AC$ ở $N.$ Cho $BM = 2cm,CN = 3cm.$ Tính $MN?$
-
A
$9cm$
-
B
$6cm$
-
C
$5cm$
-
D
$10cm$
Đáp án của giáo viên lời giải hay : A
Áp dụng tính chất 3 đường phân giác của tam giác, tia phân giác của 1 góc, hai đường thẳng song song và tính chất tam giác cân.
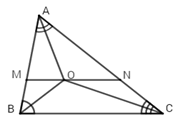
Vì O là giao điểm của hai tia phân giác của các góc \(\widehat {ABC}\) và \(\widehat {CAB}\)(gt)
Suy ra, CO là phân giác của \(\widehat {ACB}\)(tính chất 3 đường phân giác của tam giác)
\( \Rightarrow \widehat {ACO} = \widehat {BCO}\left( 1 \right)\) (tính chất tia phân giác của một góc)
BO là phân giác của \(\widehat {ABC}\left( {gt} \right) \Rightarrow \widehat {OBA} = \widehat {OBC}\left( 2 \right)\) (tính chất tia phân giác của một góc)
Vì MN // BC (gt) \(\left\{ \begin{array}{l}\widehat {MOB} = \widehat {OBC}\left( 3 \right)\\\widehat {NOC} = \widehat {OCB}\left( 4 \right)\end{array} \right.\) (so le trong)
Từ (1) và (4) \( \Rightarrow \widehat {NOC} = \widehat {NCO} \Rightarrow \Delta NOC\) cân tại N (dấu hiệu nhận biết tam giác cân)
\( \Rightarrow NO = NC = 5cm\) (tính chất tam giác cân)
Từ (2) và (3) \( \Rightarrow \widehat {MOB} = \widehat {MBO} \Rightarrow \Delta MOB\) cân tại M (dấu hiệu nhận biết tam giác cân)
\( \Rightarrow MB = MO = 4cm\) (tính chất tam giác cân)
\( \Rightarrow MN = MO + ON = 4 + 5 = 9cm.\)
Cho \(\Delta ABC\) cân tại A. Gọi G là trọng tâm của tam giác, I là giao điểm của các đường phân giác trong tam giác. Khi đó ta có:
-
A
I cách đều ba đỉnh của \(\Delta ABC\).
-
B
A, I, G thẳng hàng
-
C
G cách đều ba cạnh của \(\Delta ABC\).
-
D
Cả 3 đáp án trên đều đúng
Đáp án của giáo viên lời giải hay : B
Áp dụng tính chất:
Trong một tam giác cân, đường trung tuyến xuất phát từ đỉnh cũng đồng thời là đường phân giác ứng với cạnh đáy.
$I$ là giao điểm của các đường phân giác trong tam giác nên I cách đều 3 cạnh của tam giác. Vậy A sai
Ta có:\(\Delta ABC\) cân tại $A,I$ là giao điểm của các đường phân giác trong tam giác nên $AI$ vừa là đường trung tuyến đồng thời là đường phân giác của \(\widehat {BAC}\) . Mà $G$ là trọng tâm của \(\Delta ABC\) nên $A,G,I$ thẳng hàng. Chọn B.
Cho tam giác \(ABC\) có: \(\widehat B = 2\widehat C,\) các đường phân giác của góc \(B\) và \(C\) cắt nhau tại \(I.\) Chọn câu đúng.
-
A
\(AC = AB + IB\)
-
B
\(AC = AB + IA\)
-
C
\(AC = AB + IC\)
-
D
\(AC = BC + IB\)
Đáp án của giáo viên lời giải hay : A
+ Kẻ \(ID \bot BC;IE \bot AC;IF \bot AB\)
+ Sử dụng tính chất ba đường phân giác của tam giác, chứng minh \(AI\) là phân giác của \(\widehat {BAC}\)
+ Chứng minh \(BF = BD;\) \(AF = AE;CE = CD\)
+ Trên đoạn \(DC\) lấy điểm \(G\) sao cho \(BD = DG\), chứng minh \(IB = IG\)
+ Chứng minh \(IG//AC\)
+ Chứng minh \(IG = GC\)
+ Từ các điều trên ta tính được \(AC\).
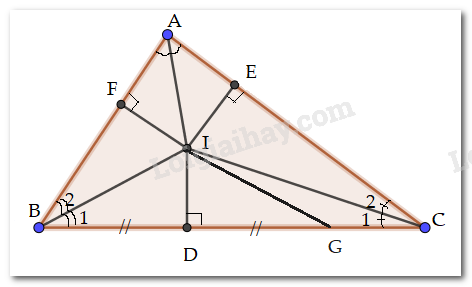
Kẻ \(ID \bot BC;IE \bot AC;IF \bot AB\)
Tam giác \(ABC\) có các đường phân giác của góc \(\widehat {ABC}\) và \(\widehat {ACB}\) cắt nhau tại \(I\) nên \(AI\) là phân giác của \(\widehat {BAC}\) (tính chất ba đường phân giác của tam giác)
Vì \(BI\) là tia phân giác của \(\widehat {ABC}\) nên \(\widehat {{B_1}} = \widehat {{B_2}} = \dfrac{{\widehat {ABC}}}{2}\) (tính chất tia phân giác)
Xét \(\Delta BFI\) vuông tại \(F\) và \(\Delta BDI\) vuông tại \(D\) có:
\(\widehat {{B_1}} = \widehat {{B_2}}\) (cmt)
\(BI\) là cạnh chung
Do đó \(\Delta BFI = \Delta BDI\) (cạnh huyền – góc nhọn) \( \Rightarrow BF = BD\) (hai cạnh tương ứng)
Chứng minh tương tự ta có: \(AF = AE;CE = CD\).
Trên đoạn \(DC\) lấy điểm \(G\) sao cho \(BD = DG\).
Xét \(\Delta BDI\) vuông tại \(D\) và \(\Delta GDI\) vuông tại \(D\) có:
\(BD = DG\) (theo cách vẽ)
\(DI\) là cạnh chung
Do đó \(\Delta BDI = \Delta GDI\) (hai cạnh góc vuông) \( \Rightarrow IB = IG\) (hai cạnh tương ứng) \( \Rightarrow \Delta IBG\) là tam giác cân tại \(I\)
\( \Rightarrow \widehat {{B_1}} = \widehat {IGB}\) (tính chất tam giác cân) \((1)\)
Ta có: \(\widehat {ABC} = 2\widehat {ACB} \Rightarrow \widehat {ACB} = \dfrac{{\widehat {ABC}}}{2} = \widehat {{B_1}}\) \((2)\)
Từ \((1)\); \((2)\) suy ra: \( \Rightarrow \widehat {IGB} = \widehat {ACB}\) mà hai góc này ở vị trí đồng vị nên \(IG//AC\) (dấu hiệu nhận biết hai đường thẳng song song)
Khi đó \(\widehat {{C_2}} = \widehat {GIC}\) (hai góc so le trong)
Mặt khác: \(\widehat {{C_2}} = \widehat {{C_1}}\) (do \(CI\) là tia phân giác của \(\widehat {ACB}\))
\( \Rightarrow \widehat {{C_1}} = \widehat {GIC} \Rightarrow \Delta GIC\) cân tại \(G\) \( \Rightarrow IG = GC\) (định nghĩa tam giác cân)
Ta có: \(AC = AE + CE\)
\(\begin{array}{l} = AF + CD\\ = AF + DG + GC\\ = AF + BD + IG\\ = AF + BF + IB\\ = AB + IB\end{array}\)
