Cho d là đường trung trực của đoạn thẳng AB. Gọi O là trung điểm của AB. Trên d lấy 2 điểm M, N sao cho OM = ON. Tứ giác AMBN là hình gì? Chọn câu trả lời đúng nhất.
-
A
Hình chữ nhật
-
B
Hình vuông
-
C
Hình thoi
-
D
Hình bình hành
Đáp án của giáo viên lời giải hay : C
Sử dụng tính chất đường trung trực của đoạn thẳng.
Áp dụng các trường hợp bằng nhau của tam giác suy ra các cạnh bằng nhau.

Vì M nằm trên đường trung trực của AB nên MA = MB ( tính chất)
Vì N nằm trên đường trung trực của AB nên NA = NB ( tính chất)
Xét tam giác AOM và AON có:
OM = ON
\(\widehat {AOM} = \widehat {AON}( = 90^\circ )\)
AO chung
\( \Rightarrow \Delta AOM = \Delta AON\) ( c.g.c)
\( \Rightarrow \) AM = AN ( 2 cạnh tương ứng)
Mà MA = MB; NA = NB
\( \Rightarrow \) MA = MB = NB = NA
\( \Rightarrow \) Tứ giác AMBN là hình thoi ( Tứ giác có 4 cạnh bằng nhau)
Cho tam giác ABC cân tại B. Kẻ đường trung trực của BA cắt AB tại H, trung trực của BC cắt AB tại H và trung trực của AC cắt AC tại L. 3 đường trung trực này cắt nhau tại I.
-
A
IH = IK
-
B
IH = IL
-
C
IH +IK = IL
-
D
IK = IL
Đáp án của giáo viên lời giải hay : A
Dựa vào tính chất tam giác cân
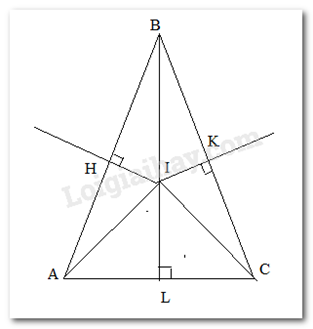
Vì tam giác ABC cân tại B nên BA = BC
Mà H, K lần lượt là trung điểm của BA và BC nên BH = BK
Xét tam giác vuộng BHI và BKI có:
BI chung
BH = BK
\( \Rightarrow BHI = \Delta BKI\) ( cạnh huyển – cạnh góc vuông)
\( \Rightarrow \) IH = IK (hai cạnh tương ứng).
