Chọn câu đúng nhất:
-
A
Nếu hai đường thẳng \(a,b\) cắt đường thẳng c tạo thành một cặp góc so le trong bằng nhau thì \(a//b.\)
-
B
Nếu hai đường thẳng \(a,b\) cắt đường thẳng c tạo thành một cặp góc đồng vị bằng nhau thì \(a//b.\)
-
C
Hai đường thẳng a, b cắt đường thẳng c và trong các góc tạo thành có một cặp góc so le ngoài bằng nhau thì \(a//b.\)
-
D
Cả A, B, C đều đúng.
Đáp án của giáo viên lời giải hay : D
Sử dụng dấu hiệu nhận biết hai đường thẳng song song
+ Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành một cặp góc so le trong bằng nhau thì hai đường thẳng song song.
+ Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành một cặp góc đồng vị bằng nhau thì hai đường thẳng song song.
+ Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành một cặp góc so le ngoài bằng nhau thì hai đường thẳng song song.
Vậy khẳng định A,B,C đều đúng.
Chọn D
Điền vào chỗ trống:
“Nếu hai đường thẳng a và b cắt đường thẳng c tạo thành một cặp góc đồng vị … thì các cặp góc so le trong bằng nhau”
-
A
bù nhau
-
B
bằng nhau
-
C
phụ nhau
-
D
kề nhau
Đáp án của giáo viên lời giải hay : B
Dựa vào tính chất các góc tạo bởi một đường thẳng cắt 2 đường thẳng.
Nếu hai đường thẳng a và b cắt đường thẳng c tạo thành một cặp góc đồng vị bằng nhau thì các cặp góc so le trong bằng nhau.
Cho hình vẽ dưới đây :
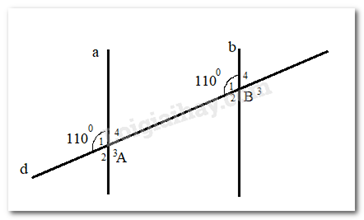
Khẳng định sai là:
-
A
\(\widehat {{A_2}} = \widehat {{B_4}}\)
-
B
\(\widehat {{A_3}} = \widehat {{B_2}}\)
-
C
\(\widehat {{A_4}} + \widehat {{B_1}} = 180^\circ \)
-
D
\(\widehat {{B_2}} = \widehat {{B_4}}\)
Đáp án của giáo viên lời giải hay : B
Dựa vào tính chất các góc tạo bởi một đường thẳng cắt 2 đường thẳng.
Vì đường thẳng d cắt 2 đường thẳng a và b tạo thành cặp góc A1 và B1 bằng nhau ( cùng bằng 110\(^\circ \)) nên:
+) \(\widehat {{A_2}} = \widehat {{B_2}}\)( 2 góc đồng vị)
Mà \(\widehat {{B_2}} = \widehat {{B_4}}\) ( 2 góc đối đỉnh)
\( \Rightarrow \widehat {{A_2}} = \widehat {{B_4}}\) nên A đúng
+) \(\widehat {{A_3}} = \widehat {{B_3}}\) ( 2 góc đồng vị)
Mà \(\widehat {{B_2}} + \widehat {{B_3}} = 180^\circ \) ( 2 góc kề bù) và \(\widehat {{A_1}} = \widehat {{A_3}}\); \(\widehat {{B_1}} = \widehat {{B_3}}\) ( 2 góc đối đỉnh) nên \(\)\(\widehat {{B_2}} + 110^\circ = 180^\circ \Rightarrow \widehat {{B_2}} = 70^\circ \)
\( \Rightarrow \widehat {{A_3}} \ne \widehat {{B_2}}\) nên B sai
+) \(\widehat {{A_1}} = \widehat {{B_1}}\)(=110\(^\circ \))
Mà \(\widehat {{A_1}} + \widehat {{A_4}} = 180^\circ \) ( 2 góc kề bù)
\( \Rightarrow \widehat {{A_4}} + \widehat {{B_1}} = 180^\circ \) nên C đúng
Ta có: \(\widehat {{B_2}} = \widehat {{B_4}}\) ( 2 góc đối đỉnh) nên D đúng
Cho hình vẽ dưới đây :
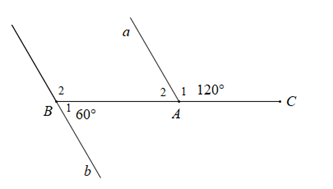
Chọn câu sai.
-
A
\(a \bot b\)
-
B
\(\widehat {{A_2}} = 60^\circ \)
-
C
\(\widehat {{B_2}} = 120^\circ \)
-
D
\(a//b\)
Đáp án của giáo viên lời giải hay : A
+ Áp dụng tính chất hai góc kề bù để tính \(\widehat {{A_2}};\,\widehat {{B_2}}.\)
+ Sử dụng dấu hiệu nhận biết để suy ra hai đường thẳng song song
Vì \(\widehat {{A_1}};\widehat {{A_2}}\) là hai góc kề bù nên \(\widehat {{A_1}} + \widehat {{A_2}} = 180^\circ \) \( \Rightarrow 120^\circ + \widehat {{A_2}} = 180^\circ \Rightarrow \widehat {{A_2}} = 60^\circ \)
Tương tự vì \(\widehat {{B_1}};\widehat {{B_2}}\) là hai góc kề bù nên \(\widehat {{B_1}} + \widehat {{B_2}} = 180^\circ \) \( \Rightarrow 60^\circ + \widehat {{B_2}} = 180^\circ \Rightarrow \widehat {{B_2}} = 120^\circ \)
Nhận thấy \(\widehat {{A_2}} = \widehat {{B_2}} = 120^\circ \) mà hai góc ở vị trí đồng vị nên \(a//b.\)
Vậy khẳng định A sai
Cho hình vẽ sau:
Em hãy chọn câu đúng nhất trong các câu sau:
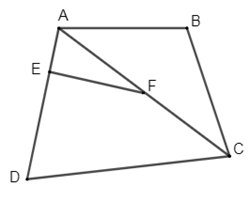
-
A
\(\widehat {AEF}\) và \(\widehat {A{\rm{D}}C}\) là hai góc đồng vị
-
B
\(\widehat {AFE}\) và \(\widehat {BAC}\) là hai góc trong cùng phía
-
C
\(\widehat {DCA}\) và \(\widehat {AFE}\) là hai góc so le trong
-
D
\(\widehat {BAC}\) và \(\widehat {DCA}\) là hai góc đồng vị
Đáp án của giáo viên lời giải hay : A
Áp dụng khái niệm hai góc đồng vị, so le trong
- \(\widehat {AEF}\) và \(\widehat {A{\rm{D}}C}\) là hai góc đồng vị (đúng, chọn A)
- \(\widehat {AFE}\) và \(\widehat {BAC}\) là hai góc trong cùng phía (sai, vì đó là hai góc so le trong) nên B sai
- \(\widehat {DCA}\) và \(\widehat {AFE}\) là hai góc so le trong (sai, vì đó là hai góc đồng vị) nên C sai
- \(\widehat {BAC}\) và \(\widehat {DCA}\) là hai góc đồng vị (sai, vì đó là hai góc so le trong) nên D sai
Chọn một cặp góc đồng vị trong hình vẽ sau:
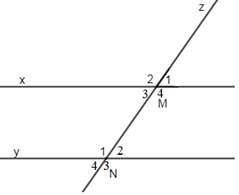
-
A
\(\widehat {{M_1}}\) và \(\widehat {{N_4}}\)
-
B
\(\widehat {{M_3}}\) và \(\widehat {{N_2}}\)
-
C
\(\widehat {{M_4}}\) và \(\widehat {{N_2}}\)
-
D
\(\widehat {{M_1}}\) và \(\widehat {{N_2}}\)
Đáp án của giáo viên lời giải hay : D
Áp dụng khái niệm hai góc đồng vị, so le trong, so le ngoài, trong cùng phía
- \(\widehat {{M_1}}\) và \(\widehat {{N_4}}\) là hai góc đồng vị (sai, vì đó là là hai góc so le ngoài) loại đáp án A.
- \(\widehat {{M_3}}\) và \(\widehat {{N_2}}\) là hai góc đồng vị (sai, vì đó là là hai góc so le trong) loại đáp án B.
- \(\widehat {{M_4}}\) và \(\widehat {{N_2}}\) là hai góc đồng vị (sai, vì đó là là hai góc trong cùng phía) loại đáp án C.
- \(\widehat {{M_1}}\) và \(\widehat {{N_2}}\) là hai góc đồng vị (đúng) chọn đáp án D.
Cho hình vẽ:

Biết \(\widehat {CF{\rm{E}}} = {55^0},\,\widehat {{E_1}} = {125^0}\) . Khi đó:
-
A
\(\widehat {AEF} = 125^\circ \)
-
B
\(AB//C{\rm{D}}\)
-
C
Cả A, B đều đúng
-
D
Cả A, B đều sai
Đáp án của giáo viên lời giải hay : C
Áp dụng dấu hiệu nhận biết hai đường thẳng song song: Nếu đường thẳng \(c\) cắt hai đường thẳng \(a\) và \(b,\) trong các góc tạo thành có \(1\) cặp góc so le trong bằng nhau thì \(a//b\).
Ta có:\(\widehat{AEF} = \widehat {{E_1}}\) ( 2 góc đối đỉnh) nên \(\widehat{AEF} = 125^0\)
Vì \(\widehat {{E_1}}\) và \(\widehat {BEF}\) là hai góc kề bù
\( \Rightarrow \widehat {{E_1}} + \widehat {BEF} = {180^0} \Rightarrow \widehat {BEF} = {180^0} - \widehat {{E_1}} = {180^0} - {125^0} = {55^0} \Rightarrow \widehat {BEF} = \widehat {CFE} = {55^0}\)
Mà \(\widehat {BEF}\) và \(\widehat {CFE}\) ở vị trí so le trong nên suy ra \(AB//C{\rm{D}}\) (dấu hiệu nhận biết hai đường thẳng song song)
Vẽ \(\Delta ABC\). Qua A vẽ đường thẳng d1 vuông góc với AB; đường thẳng d2 đi qua C và vuông góc với d1. Phát biểu nào sau đây là đúng?
-
A
d1\( \bot \)AC
-
B
AB // d2
-
C
d1 // AC
-
D
d1 \( \bot \)BC
Đáp án của giáo viên lời giải hay : B
Vẽ hình và chứng minh sự vuông góc hay song song của d1 , d2 với các đường thẳng khác.
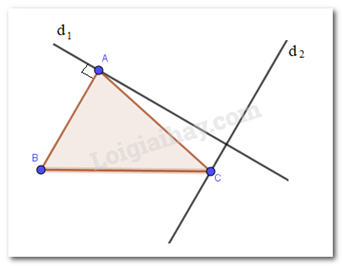
Vì AB và d2 cùng vuông góc với d1 nên AB // d2
Cho hình vẽ sau:
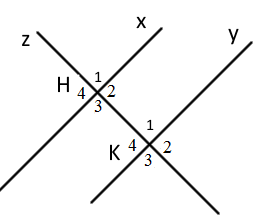
Em hãy chọn phát biểu đúng trong các phát biểu sau:
-
A
.\(\widehat {\;{H_1}}\) và \(\widehat {\;{K_1}}\) là hai góc so le trong
-
B
\(\widehat {\;\;{H_4}}\) và \(\widehat {\;{K_4}}\) là hai góc đồng vị
-
C
\(\widehat {\;{H_3}}\) và \(\widehat {{K_4}}\) là hai góc so le ngoài
-
D
\(\widehat {\;{H_4}}\) và \(\widehat {\;{K_2}}\) là hai góc so le trong
Đáp án của giáo viên lời giải hay : B
Áp dụng khái niệm hai góc đồng vị, so le trong, so le ngoài, trong cùng phía.
\(\widehat {{H_1}}\) và \(\widehat {{K_1}}\) là hai góc so le trong (sai, vì đó là 2 góc đồng vị, loại đáp án A)
\(\widehat {{H_4}}\) và \(\widehat {{K_4}}\) là hai góc đồng vị (đúng, chọn B)
\(\widehat {{H_3}}\) và \(\widehat {{K_4}}\) là hai góc so le ngoài (sai, vì đó là 2 góc trong cùng phía, loại đáp án C)
\(\widehat {{H_4}}\) và \(\widehat {{K_2}}\) là hai góc so le trong (sai, vì đó là 2 góc so le ngoài, loại đáp án D)
Biết một cặp góc so le trong \(\widehat {{A_3}} = \widehat {{B_2}} = {35^0}\). Tính số đo của cặp góc so le trong còn lại.
-
A
\({115^0}\)
-
B
\({55^0}\)
-
C
\({135^0}\)
-
D
\({145^0}\)
Đáp án của giáo viên lời giải hay : D
Áp dụng tính chất: Nếu đường thẳng c cắt hai đường thẳng a, b và trong các góc tạo thành có một cặp góc so le trong bằng nhau thì hai góc so le trong còn lại bằng nhau.

Ta có: \(\widehat {{A_3}} + \widehat {{A_4}} = {180^0}\) (kề bù)
\( \Rightarrow \widehat {{A_4}} = {180^0} - \widehat {{A_3}} = {180^0} - {35^0} = {145^0}\)
Ta có: \(\widehat {{A_3}}\) và \(\widehat {{B_2}}\); \(\widehat {{A_4}}\) và \(\widehat {{B_1}}\) là 2 cặp góc so le trong
Mặt khác, đường thẳng d cắt 2 đường thẳng x và y tạo thành 1 cặp góc so le trong \(\widehat {{A_3}} = \widehat {{B_2}} = {35^0}\) nên cặp góc so le trong còn lại cũng bằng nhau
\( \Rightarrow \widehat {{A_4}} = \widehat {{B_1}} = {145^0}.\)
Cho hình vẽ sau:
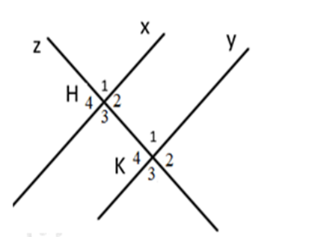
Chọn phát biểu đúng.
-
A
\(\widehat {\;{H_1}}\) và \(\widehat {\;{K_1}}\) là hai góc so le trong
-
B
\(\widehat {\;\;{H_4}}\) và \(\widehat {\;{K_4}}\) là hai góc đồng vị
-
C
\(\widehat {\;{H_3}}\) và \(\widehat {{K_4}}\) là hai góc so le ngoài
-
D
\(\widehat {\;{H_4}}\) và \(\widehat {\;{K_2}}\) là hai góc so le trong.
Đáp án của giáo viên lời giải hay : B
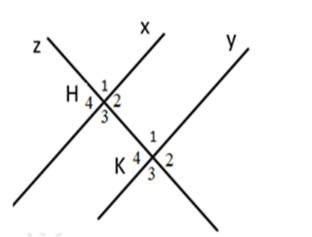
\(\widehat {{H_1}}\) và \(\widehat {{K_1}}\) là hai góc so le trong (sai, vì đó là 2 góc đồng vị, loại đáp án A)
\(\widehat {{H_4}}\) và \(\widehat {{K_4}}\) là hai góc đồng vị (đúng, chọn B)
\(\widehat {{H_3}}\) và \(\widehat {{K_4}}\) là hai góc so le ngoài (sai, vì đó là 2 góc trong cùng phía, loại đáp án C)
\(\widehat {{H_4}}\) và \(\widehat {{K_2}}\) là hai góc so le trong (sai, vì đó là 2 góc so le ngoài, loại đáp án D)
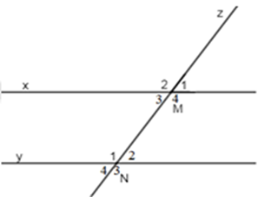
Chọn một cặp góc đồng vị trong hình vẽ sau:
-
A
\(\widehat {{M_1}}\) và \(\widehat {{N_4}}\)
-
B
\(\widehat {{M_3}}\) và \(\widehat {{N_2}}\)
-
C
\(\widehat {{M_4}}\) và \(\widehat {{N_2}}\)
-
D
\(\widehat {{M_1}}\) và \(\widehat {{N_2}}\)
Đáp án của giáo viên lời giải hay : D
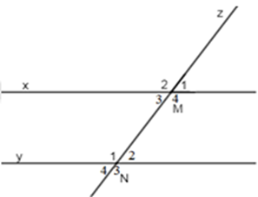
\(\widehat {{M_1}}\) và \(\widehat {{N_4}}\) là hai góc đồng vị (sai, vì đó là là hai góc so le ngoài) loại đáp án A.
\(\widehat {{M_3}}\) và \(\widehat {{N_2}}\) là hai góc đồng vị (sai, vì đó là là hai góc so le trong) loại đáp án B.
\(\widehat {{M_4}}\) và \(\widehat {{N_2}}\) là hai góc đồng vị (sai, vì đó là là hai góc trong cùng phía) loại đáp án C.
\(\widehat {{M_1}}\) và \(\widehat {{N_2}}\) là hai góc đồng vị (đúng) chọn đáp án D.
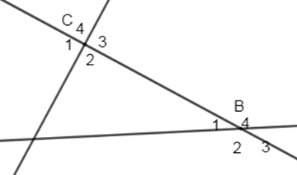
Chọn một cặp góc so le trong trong hình vẽ sau:
-
A
\(\widehat {{C_3}}\) và \(\widehat {{B_1}}\)
-
B
\(\widehat {{C_1}}\) và \(\widehat {{B_1}}\)
-
C
\(\widehat {{C_4}}\) và \(\widehat {{B_4}}\)
-
D
\(\widehat {{C_2}}\) và \(\widehat {{B_1}}\)
Đáp án của giáo viên lời giải hay : A
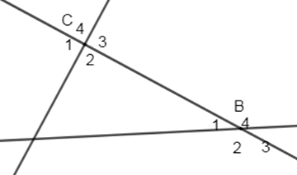
\(\widehat {{C_3}}\) và \(\widehat {{B_1}}\) là hai góc so le trong (đúng) chọn A
\(\widehat {{C_1}}\) và \(\widehat {{B_1}}\) là hai góc so le trong (sai, vì đây là 2 góc đồng vị), loại B
\(\widehat {{C_4}}\) và \(\widehat {{B_4}}\) là hai góc so le trong (sai, vì đây là 2 góc đồng vị), loại C
\(\widehat {{C_2}}\) và \(\widehat {{B_1}}\) là hai góc so le trong (sai, vì đây là 2 góc trong cùng phía), loại D.
Nếu đường thẳng c cắt hai đường thẳng a, b và trong các góc tạo thành có một cặp góc so le trong bằng nhau thì:
-
A
Hai góc trong cùng phía bằng nhau
-
B
Hai góc đồng vị bằng nhau
-
C
Hai góc so le trong còn lại có tổng bằng \({120^0}\)
-
D
Tất cả các đáp án trên đều đúng
Đáp án của giáo viên lời giải hay : B
Áp dụng tính chất: Nếu đường thẳng c cắt hai đường thẳng a, b và trong các góc tạo thành có một cặp góc so le trong bằng nhau thì:
+) Hai góc so le trong còn lại bằng nhau.
+) Hai góc đồng vị bằng nhau.
Nếu đường thẳng $c$ cắt hai đường thẳng $a,b$ và trong các góc tạo thành có một cặp góc so le trong bằng nhau thì: hai góc đồng vị bằng nhau
Cho hình vẽ sau:
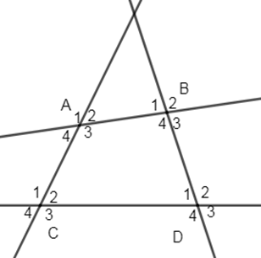
Có bao nhiêu cặp góc đồng vị?
-
A
$4$
-
B
$12$
-
C
$8$
-
D
$16$
Đáp án của giáo viên lời giải hay : D
Các cặp góc đồng vị là: \(\widehat {{A_1}}\) và \(\widehat {{C_1}}\), \(\widehat {{A_4}}\) và \(\widehat {{C_4}}\), \(\widehat {{A_2}}\) và \(\widehat {{C_2}}\), \(\widehat {{A_3}}\) và \(\widehat {{C_3}}\), \(\widehat {{B_1}}\) và \(\widehat {{D_1}}\), \(\widehat {{B_2}}\) và \(\widehat {{D_2}}\), \(\widehat {{B_3}}\) và \(\widehat {{D_3}}\), \(\widehat {{B_4}}\) và \(\widehat {{D_4}}\).
Tương tự ta có thêm $8$ cặp góc đồng vị \(\widehat {{A_1}}\) và \(\widehat {{B_1}}\), \(\widehat {{A_4}}\) và \(\widehat {{B_4}}\), \(\widehat {{A_2}}\) và \(\widehat {{B_2}}\), \(\widehat {{A_3}}\) và \(\widehat {{B_3}}\), \(\widehat {{C_1}}\) và \(\widehat {{D_1}}\), \(\widehat {{C_2}}\) và \(\widehat {{D_2}}\), \(\widehat {{C_3}}\) và \(\widehat {{D_3}}\), \(\widehat {{C_4}}\) và \(\widehat {{D_4}}\).
Biết một cặp góc so le trong \(\widehat {{A_3}} = \widehat {{B_2}} = {35^0}\). Tính số đo của cặp góc so le trong còn lại.
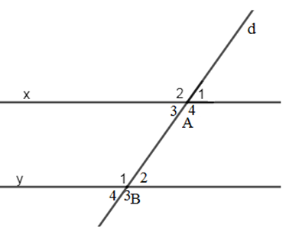
-
A
\({115^0}\)
-
B
\({55^0}\)
-
C
\({135^0}\)
-
D
\({145^0}\)
Đáp án của giáo viên lời giải hay : D
Áp dụng tính chất: Nếu đường thẳng c cắt hai đường thẳng a, b và trong các góc tạo thành có một cặp góc so le trong bằng nhau thì hai góc so le trong còn lại bằng nhau.
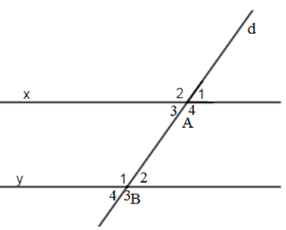
Ta có: \(\widehat {{A_3}} + \widehat {{A_4}} = {180^0}\) (kề bù)
\( \Rightarrow \widehat {{A_4}} = {180^0} - \widehat {{A_3}} = {180^0} - {35^0} = {145^0}\)
Ta có: \(\widehat {{A_3}}\) và \(\widehat {{B_2}}\); \(\widehat {{A_4}}\) và \(\widehat {{B_1}}\) là 2 cặp góc so le trong
Mặt khác, đường thẳng d cắt 2 đường thẳng x và y tạo thành 1
cặp góc so le trong \(\widehat {{A_3}} = \widehat {{B_2}} = {35^0}\)nên \( \Rightarrow \widehat {{A_4}} = \widehat {{B_1}} = {145^0}.\)
Cho hình vẽ sau:
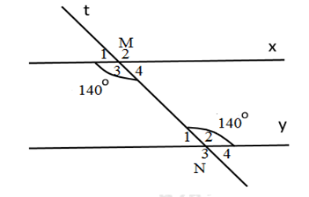
Biết \(\widehat {{M_3}} = \widehat {{N_2}} = {140^0}.\) Tính \(\widehat {{M_4}} + \widehat {{N_2}},\,\widehat {{M_3}} + \widehat {{N_1}}.\)
-
A
\({115^0}\)
-
B
\({55^0}\)
-
C
\({180^0}\)
-
D
\({145^0}\)
Đáp án của giáo viên lời giải hay : C
Áp dụng tính chất: Tổng hai góc kề bù bằng \({180^0}\).
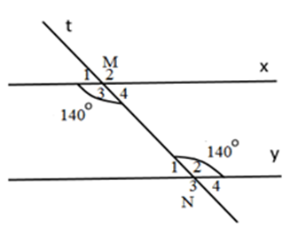
Ta có: \(\widehat {{M_3}} + \widehat {{M_4}} = {180^0}\) (kề bù)
\(\begin{array}{l} \Rightarrow \widehat {{M_4}} = {180^0} - \widehat {{M_3}} = {180^0} - {140^0} = {40^0}\\ \Rightarrow \widehat {{M_4}} + \,\widehat {{N_2}} = {40^0} + {140^0} = {180^0}\end{array}\)
Ta có: \(\widehat {{N_2}} + \widehat {{N_1}} = {180^0}\) (kề bù)
\(\begin{array}{l} \Rightarrow \widehat {{N_1}} = {180^0} - \widehat {{N_2}} = {180^0} - {140^0} = {40^0}\\ \Rightarrow \widehat {{M_3}} + \widehat {{N_1}} = {140^0} + {40^0} = {180^0}\end{array}\)
Cho hình vẽ sau:
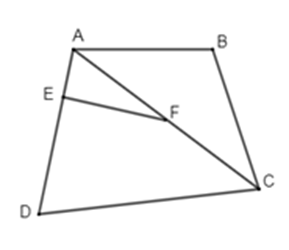
Em hãy chọn câu đúng nhất trong các câu sau:
-
A
\(\widehat {AEF}\) và \(\widehat {A{\rm{D}}C}\) là hai góc đồng vị
-
B
$\widehat {AFE}$ và \(\widehat {BAC}\) là hai góc trong cùng phía
-
C
\(\widehat {DCA}\) và $\widehat {AFE}$ là hai góc so le trong
-
D
\(\widehat {BAC}\) và \(\widehat {DCA}\) là hai góc đồng vị
Đáp án của giáo viên lời giải hay : A
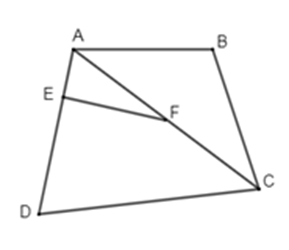
- \(\widehat {AEF}\) và \(\widehat {A{\rm{D}}C}\) là hai góc đồng vị (đúng, chọn A)
- $\widehat {AFE}$ và \(\widehat {BAC}\) là hai góc trong cùng phía (sai, vì đó là hai góc so le trong) loại B
- \(\widehat {DCA}\) và $\widehat {AFE}$ là hai góc so le trong (sai, vì đó là hai góc đồng vị) loại C
- \(\widehat {BAC}\) và \(\widehat {DCA}\) là hai góc đồng vị (sai, vì đó là hai góc so le trong) loại D
Tính giá trị \(x;y;z;t\) trên hình sau:
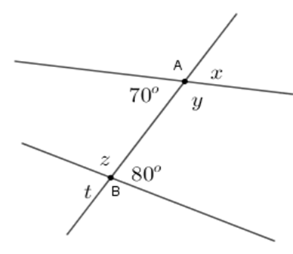
-
A
$x = {80^o};y = {110^0};z = {100^o};t = {70^o}$
-
B
$x = {70^o};y = {100^0};z = {110^o};t = {80^o}$
-
C
$x = {70^o};y = {110^0};z = {100^o};t = {80^o}$ \(\)
-
D
$x = {70^o};y = {100^0};z = {100^o};t = {80^o}$
Đáp án của giáo viên lời giải hay : C
Sử dụng tổng hai góc kề bù bằng \({180^o}\) , tính chất hai góc đối đỉnh
Ta có \(x = {70^0}\) (tính chất hai góc đối đỉnh)
\(y + {70^o} = {180^o} \Rightarrow y = {110^o}\) (hai góc kề bù)
Tương tự ta có \(t = {80^o};\,z = {100^o}\)
Vậy $x = {70^o};y = {110^0};z = {100^o};t = {80^o}.$
Cho hình vẽ sau:
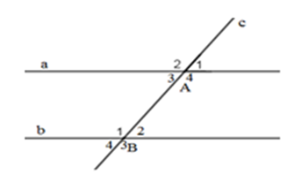
Biết \(\widehat {{A_3}} = \widehat {{B_2}} = {30^0}\). Tính số đo góc \({A_4}\) và góc \({B_1}.\)
-
A
\(\widehat {{A_4}} = \widehat {{B_1}} = {150^0}\)
-
B
\(\widehat {{A_4}} = \widehat {{B_1}} = {120^0}\)
-
C
\(\widehat {{A_4}} = {120^o};\widehat {{B_1}} = {150^0}\) \(\)
-
D
\(\widehat {{A_4}} = \widehat {{B_1}} = {100^0}\)
Đáp án của giáo viên lời giải hay : A
Áp dụng tính chất: Nếu đường thẳng c cắt hai đường thẳng a, b và trong các góc tạo thành có một cặp góc so le trong bằng nhau thì:
+) Hai góc so le trong còn lại bằng nhau.
+) Hai góc đồng vị bằng nhau.
Cặp góc so le trong còn lại là: \(\widehat {{A_4}}\) và \(\widehat {{B_1}}\).
Ta có: \(\widehat {{A_3}} + \widehat {{A_4}} = {180^0}\) (kề bù)
\(\begin{array}{l} \Rightarrow \widehat {{A_4}} = {180^0} - \widehat {{A_3}} = {180^0} - {30^0} = {150^0}\\ \Rightarrow \widehat {{A_4}} = \widehat {{B_1}} = {150^0}\end{array}\)
Chọn câu trả lời đúng trong các câu sau: Trong mặt phẳng,
-
A
Hai đường thẳng không có điểm chung thì song song với nhau.
-
B
Hai đoạn thẳng có điểm chung thì song song với nhau.
-
C
Hai đường thẳng có hai điểm chung thì song song với nhau.
-
D
Hai đường thẳng song song là hai đường thẳng không trùng nhau.
Đáp án của giáo viên lời giải hay : A
Hai đường thẳng song song (trong mặt phẳng) là hai đường thẳng không có điểm chung.
Chọn câu đúng nhất.
-
A
Nếu hai đường thẳng $a,b$ cắt đường thẳng c tạo thành một cặp góc so le trong bằng nhau thì $a//b.$
-
B
Nếu hai đường thẳng $a,b$ cắt đường thẳng c tạo thành một cặp góc đồng vị bằng nhau thì $a//b.$
-
C
Hai đường thẳng a, b cắt đường thẳng c và trong các góc tạo thành có một cặp góc so le ngoài bằng nhau thì \(a//b.\)
-
D
Cả A, B, C đều đúng.
Đáp án của giáo viên lời giải hay : D
+ Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành một cặp góc so le trong bằng nhau thì hai đường thẳng song song.
+ Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành một cặp góc đồng vị bằng nhau thì hai đường thẳng song song.
+ Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành một cặp góc so le ngoài bằng nhau thì hai đường thẳng song song.
nên cả A, B, C đều đúng.
Cho hình vẽ dưới đây :
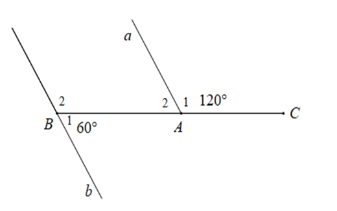
Chọn câu sai.
-
A
\(a \bot b\)
-
B
\(\widehat {{A_2}} = 60^\circ \)
-
C
\(\widehat {{B_2}} = 120^\circ \)
-
D
\(a//b\)
Đáp án của giáo viên lời giải hay : A
+ Áp dụng tính chất hai góc kề bù để tính \(\widehat {{A_2}};\,\widehat {{B_2}}.\)
+ Sử dụng dấu hiệu nhận biết để suy ra hai đường thẳng song song
Vì \(\widehat {{A_1}};\widehat {{A_2}}\) là hai góc kề bù nên \(\widehat {{A_1}} + \widehat {{A_2}} = 180^\circ \) \( \Rightarrow 120^\circ + \widehat {{A_2}} = 180^\circ \Rightarrow \widehat {{A_2}} = 60^\circ \)
Tương tự vì \(\widehat {{B_1}};\widehat {{B_2}}\) là hai góc kề bù nên \(\widehat {{B_1}} + \widehat {{B_2}} = 180^\circ \) \( \Rightarrow 60^\circ + \widehat {{B_2}} = 180^\circ \Rightarrow \widehat {{B_2}} = 120^\circ \)
Nhận thấy \(\widehat {{A_2}} = \widehat {{B_2}} = 120^\circ \) mà hai góc ở vị trí đồng vị nên \(a//b.\)
Vậy A sai.
Cho hình vẽ:
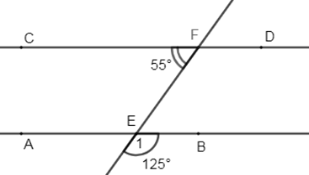
Biết \(\widehat {CF{\rm{E}}} = {55^0},\,\widehat {{E_1}} = {125^0}\) . Khi đó:
-
A
\(\widehat {AEF} = 125^\circ \)
-
B
\(AB//C{\rm{D}}\)
-
C
Cả A, B đều đúng
-
D
Cả A, B đều sai
Đáp án của giáo viên lời giải hay : C
Áp dụng dấu hiệu nhận biết hai đường thẳng song song: Nếu đường thẳng $c$ cắt hai đường thẳng $a$ và $b,$ trong các góc tạo thành có $1$ cặp góc so le trong bằng nhau thì \(a//b\).
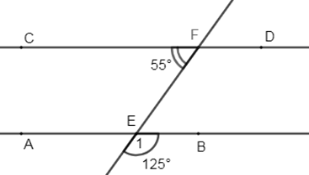
Vì \(\widehat {{E_1}}\) và \(\widehat {BEF}\) là hai góc kề bù (gt)
\( \Rightarrow \widehat {{E_1}} + \widehat {BEF} = {180^0} \)\(\Rightarrow \widehat {BEF} = {180^0} - \widehat {{E_1}} \)\(= {180^0} - {125^0} = {55^0} \)\(\Rightarrow \widehat {BEF} = \widehat {CFE} = {55^0}\)
Mà \(\widehat {BEF}\) và \(\widehat {CFE}\) là hai góc so le trong nên suy ra \(AB//C{\rm{D}}\) (dấu hiệu nhận biết hai đường thẳng song song)
Lại có \(\widehat {{E_1}}=\widehat {{AEF}}\) (hai góc đối đỉnh) nên \(\widehat {{AEF}}=125^0\)
Vậy cả A, B đều đúng.
