Kết quả phân tích đa thức \({x^2} + xy-x-y\;\) thành nhân tử là:
-
A
\(\left( {x + y} \right)\left( {x-1} \right)\)
-
B
\(\left( {x + y} \right)\left( {x + 1} \right)\;\;\)
-
C
\(\left( {x-y} \right)\left( {x-1} \right)\)
-
D
\(\left( {x-y} \right)\left( {x + 1} \right)\)
Đáp án của giáo viên lời giải hay : A
Sử dụng phương pháp nhóm hạng tử để phân tích đa thức thành nhân tử.
\({x^2} + xy - x - y = x\left( {x + y} \right) - \left( {x + y} \right)\)\( = \left( {x - 1} \right)\left( {x + y} \right)\).
Phương trình \((2x - 4)(2x - 1) = 0\) có tập nghiệm là:
-
A
\(\left\{ 1 \right\}\)
-
B
\(\left\{ {2;\dfrac{1}{2}} \right\}\)
-
C
\(\left\{ 2 \right\}\)
-
D
\(\left\{ { - 1;2} \right\}\)
Đáp án của giáo viên lời giải hay : B
Sử dụng \(A\left( x \right). B\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}A\left( x \right) = 0\\B\left( x \right) = 0\end{array} \right.\)
Ta có: \((2x - 4)(2x - 1) = 0 \Leftrightarrow \left[ \begin{array}{l}2x - 4 = 0\\2x - 1 = 0\end{array} \right.\)\( \Leftrightarrow \left[ \begin{array}{l}2x = 4\\2x = 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 2\\x = \dfrac{1}{2}\end{array} \right.\)
Vậy phương trình đã cho có tập nghiệm \(S = \left\{ {\dfrac{1}{2};2} \right\}\).
Cho \(a \le b\). Khẳng định nào sau đây là sai?
-
A
\( - \dfrac{3}{4}a \le - \dfrac{3}{4}b\)
-
B
\(\dfrac{1}{2}a \le \dfrac{1}{2}b\)
-
C
\( - 5a \ge - 5b\)
-
D
\(a - 7 \le b - 7\)
Đáp án của giáo viên lời giải hay : A
Sử dụng liên hệ giữa thứ tự và phép nhân:
+ Khi nhân hai vế của bất phương trình với một số dương thì ta giữ nguyên dấu bất phương trình.
+ Khi nhân hai vế của bất phương trình với một số âm thì ta đổi dấu bất phương trình.
Sử dụng liên hệ giữa thứ tự và phép cộng: Khi cộng hai vế của bất phương trình cùng một số thì ta giữ nguyên dấu bất phương trình.
Ta có: \(a \le b \Leftrightarrow - \dfrac{3}{4}a \ge - \dfrac{3}{4}b\) (vì \( - \dfrac{3}{4} < 0\)) nên A sai.
Vì \(a \le b \Leftrightarrow \dfrac{1}{2}a \le \dfrac{1}{2}b\) (vì \(\dfrac{1}{2} > 0\)) nên B đúng.
Vì \(a \le b \Leftrightarrow - 5a \ge - 5b\) (vì \( - 5 < 0\)) nên C đúng.
Vì \(a \le b \Leftrightarrow a + \left( { - 7} \right) \le b + \left( { - 7} \right)\)\( \Leftrightarrow a - 7 < b - 7\) nên D đúng.
Một hình hộp chữ nhật có thể tích \(192cm^3,\) mặt đáy có chiều dài 6cm và chiều rộng $4cm.$ Chiều cao hình hộp chữ nhật đó là:
-
A
\(7\,cm\)
-
B
\(9\,cm\)
-
C
\(6\,cm\)
-
D
\(8\,cm\)
Đáp án của giáo viên lời giải hay : D
Sử dụng công thức tính thể tích hình hộp chữ nhật có chiều dài, chiều rộng và chiều cao lần lượt là \(a,b,c\) là \(V = abc.\)
Hình hộp chữ nhật có chiều dài \(a = 6cm,\) chiều rộng \(b = 4cm\) và chiều cao \(c.\)
Thể tích hình hộp chữ nhật \(V = abc\) \( = 6.4.c\)
Theo đề bài ta có \(6.4.c = 192 \Leftrightarrow c = 8\,cm.\)
Vậy chiều cao cần tìm là \(8\,cm.\)
Điều kiện xác định của phương trình: \(\dfrac{{3x + 2}}{{x + 2}} + \dfrac{{2x - 11}}{{{x^2} - 4}} = \dfrac{3}{{2 - x}}\) là:
-
A
\(x \ne \dfrac{{ - 2}}{3};x \ne \dfrac{{11}}{2}\)
-
B
\(x \ne 2\)
-
C
\(x > 0\)
-
D
\(x \ne 2\) và \(x \ne - 2\)
Đáp án của giáo viên lời giải hay : D
Phương trình chứa ẩn ở mẫu có nghĩa khi các mẫu thức đều khác $0.$
Để phương trình có nghĩa: \(\left\{ \begin{array}{l}x + 2 \ne 0\\2 - x \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ne - 2\\x \ne 2\end{array} \right..\)
Vậy điều kiện xác định của phương trình là: \(x \ne 2,\;x \ne - 2.\)
\(x = - 2\) là một nghiệm của bất phương trình nào dưới đây?
-
A
\(3x + 17 < 5\)
-
B
\( - 2x + 1 < - 1\)
-
C
\(\dfrac{1}{2}x + 5 > 3,5\)
-
D
\(1 - 2x < - 3\)
Đáp án của giáo viên lời giải hay : C
Giải từng bất đẳng thức trong 4 đáp án, chọn đáp án mà bất đẳng thức có nghiệm \(x = - 2\) nằm trong tập nghiệm.
Xét từng đáp án ta có:
\(3x + 17 < 5 \Leftrightarrow 3x < - 12 \Leftrightarrow x < - 4 \Rightarrow \) A sai.
\( - 2x + 1 < - 1 \Leftrightarrow - 2x < - 2 \Leftrightarrow x > 1 \Rightarrow \) B sai.
\(\dfrac{1}{2}x + 5 > 3,5 \Leftrightarrow \dfrac{1}{2}x > - 1,5 \Leftrightarrow x > - 3 \Rightarrow x = - 2\) là một nghiệm của bất phương trình \( \Rightarrow \) C đúng.
\(1 - 2x < - 3 \Leftrightarrow - 2x < - 4 \Leftrightarrow x > 2 \Rightarrow \) D sai.
Phương trình \(\left| {2x + 5} \right| - 3 = x\) có nghiệm là:
-
A
\(\left\{ { - 8;\dfrac{{ - 2}}{3}} \right\}\)
-
B
\(\left\{ { - 8;\dfrac{2}{3}} \right\}\)
-
C
\(\left\{ { - 2;\dfrac{{ - 8}}{3}} \right\}\)
-
D
\(\left\{ { - 2;\dfrac{8}{3}} \right\}\)
Đáp án của giáo viên lời giải hay : C
Chuyển vế đưa phương trình về dạng \(\left| A \right| = B\,\,\left( {B \ge 0} \right) \Leftrightarrow \left[ \begin{array}{l}A = B\\A = - B\end{array} \right.\)
\(\begin{array}{l}\;\;\;\;\left| {2x + 5} \right| - 3 = x\\ \Leftrightarrow \left| {2x + 5} \right| = x + 3\,\,\,\left( {x \ge - 3} \right)\\ \Leftrightarrow \left[ \begin{array}{l}2x + 5 = x + 3\\2x + 5 = - \left( {x + 3} \right)\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = - 2\\2x + 5 = - x - 3\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = - 2\\3x = - 8\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = - 2\,(tm)\\x = - \dfrac{8}{3}\,(tm)\end{array} \right.\end{array}\) \(\)
Vậy tập nghiệm của phương trình là S = \(\left\{ { - 2;\dfrac{{ - 8}}{3}} \right\}\).\(\)
Cho AD là phân giác của \(\Delta ABC\left( {D \in BC} \right)\) có \(AB = 14cm, AC = 21cm, BD = 8cm.\) Độ dài cạnh BC là:
-
A
\(15\,cm\)
-
B
\(18\,cm\)
-
C
\(20\,cm\)
-
D
\(22\,cm\)
Đáp án của giáo viên lời giải hay : C
Áp dụng tính chất đường phân giác của một tam giác.
Đường phân giác trong của một tam giác chia cạnh đối diện thành hai đoạn thẳng tương ứng tỉ lệ với hai cạnh kề hai đoạn thẳng đó.
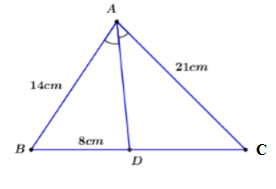
Vì AD là phân giác của tam giác ABC, theo tính chất của đường phân giác ta có:
\(\begin{array}{l}\dfrac{{AB}}{{B{\rm{D}}}} = \dfrac{{AC}}{{C{\rm{D}}}} \Leftrightarrow \dfrac{{14}}{8} = \dfrac{{21}}{{C{\rm{D}}}} \Leftrightarrow C{\rm{D}} = \dfrac{{8.21}}{{14}} = 12cm\\ \Rightarrow BC = B{\rm{D}} + DC = 8 + 12 = 20cm\end{array}\).
Cho \(\Delta ABC\) và \(MN//BC\) với M nằm giữa A và B, N nằm giữa A và C. Biết \(AN = 2cm, AB = 3AM.\) Kết quả nào sau đây đúng:
-
A
\(AC = 6cm\)
-
B
\(CN = 3cm\)
-
C
\(AC = 9cm\)
-
D
\(CN = 1,5cm\)
Đáp án của giáo viên lời giải hay : A
Áp dụng định lý Ta-let: “Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ”.
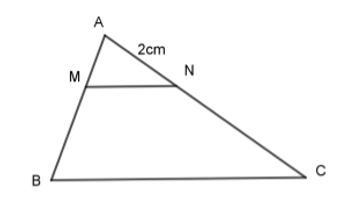
Theo bài ta có: \(AB = 3AM \Rightarrow \dfrac{{AM}}{{AB}} = \dfrac{1}{3}\).
Vì \(MN//BC,\) theo định lý Ta-let ta có:
\(\dfrac{{AM}}{{AB}} = \dfrac{{AN}}{{AC}} \Leftrightarrow \dfrac{1}{3} = \dfrac{2}{{AC}} \Leftrightarrow AC = 2. 3 = 6cm\).
Cho \(\Delta ABC\) đồng dạng với \(\Delta A'B'C'\) theo tỉ số \(\dfrac{3}{5}\) và chu vi của \(\Delta A'B'C'\) là $60cm.$ Khi đó chu vi \(\Delta ABC\) là:
-
A
\(20\,cm\)
-
B
\(24\,cm\)
-
C
\(36\,cm\)
-
D
\(30\,cm\)
Đáp án của giáo viên lời giải hay : C
Ta có: \(\Delta ABC \backsim \Delta A'B'C'\) theo tỉ số \(k\)\( \Rightarrow \dfrac{{{C_{\Delta ABC}}}}{{{C_{\Delta A'B'C'}}}} = \dfrac{{AB}}{{A'B'}} = k.\)
Cho \(\Delta ABC\) đồng dạng với \(\Delta A'B'C'\) theo tỉ số \(\dfrac{3}{5}\).
\( \Rightarrow \dfrac{{AB}}{{A'B'}} = \dfrac{{BC}}{{B'C'}} = \dfrac{{AC}}{{A'C'}} = \dfrac{3}{5}\)\( \Rightarrow \dfrac{{{C_{\Delta ABC}}}}{{{C_{\Delta A'B'C'}}}} = \dfrac{3}{5} \Rightarrow {C_{\Delta ABC}} = \dfrac{3}{5}{C_{\Delta A'B'C'}}.\)
Mà chu vi của tam giác \({C_{\Delta A'B'C'}} = 60cm\) nên \({C_{\Delta ABC}} = \dfrac{3}{5}. 60 = 36cm\).
Cho các biểu thức \(A = \dfrac{{2x - 1}}{{x + 3}}\) và \(B = \dfrac{2}{{{x^2} - 9}}\) (với \(x \ne \pm 3\)).
Tìm $x$ để \(A = \dfrac{3}{2}\).
-
A
\(x = - 11\)
-
B
\(x = 9\)
-
C
\(x = 11\)
-
D
\(x = 10\)
Đáp án của giáo viên lời giải hay : C
Thế biểu thức chứa ẩn x vào biểu thức A.
Giải phương trình chứa ẩn ở mẫu, tìm x thỏa mãn.
Điều kiện: \(x \ne - 3.\)
\(\begin{array}{l}A = \dfrac{3}{2} \Leftrightarrow \dfrac{{2x - 1}}{{x + 3}} = \dfrac{3}{2}\\ \Rightarrow \left( {2x - 1} \right).2 = 3.\left( {x + 3} \right)\\ \Leftrightarrow 4x - 2 = 3x + 9\\ \Leftrightarrow 4x - 3x = 9 + 2\\ \Leftrightarrow x = 11\;\;\;(tm)\end{array}\).
Vậy \(x = 11\) thì \(A = \dfrac{3}{2}.\)
Tìm \(x\) để \(\dfrac{A}{B} < {x^2} + 5\).
-
A
\(x < - 1\)
-
B
\(x > - 1\)
-
C
\(x \ge - 1\)
-
D
\(x > - 1\) và \(x \ne 3\)
Đáp án của giáo viên lời giải hay : D
Thế biểu thức chứa ẩn x vào biểu thức A và B tương ứng.
Biến đổi và giải bất phương trình thu được.
Điều kiện: \(x \ne \pm 3.\)
Ta có: \(\dfrac{A}{B} = \dfrac{{2x - 1}}{{x + 3}}:\dfrac{2}{{{x^2} - 9}} = \dfrac{{2x - 1}}{{x + 3}}.\dfrac{{\left( {x - 3} \right)\left( {x + 3} \right)}}{2} = \dfrac{{\left( {2x - 1} \right)\left( {x - 3} \right)}}{2}.\)
\(\begin{array}{l} \Rightarrow \dfrac{A}{B} < {x^2} + 5 \Leftrightarrow \dfrac{{\left( {2x - 1} \right)\left( {x - 3} \right)}}{2} < {x^2} + 5\\ \Leftrightarrow 2{x^2} - 6x - x + 3 < 2{x^2} + 10\\ \Leftrightarrow 7x > - 7 \Leftrightarrow x > - 1.\end{array}\)
Kết hợp với điều kiện \(x \ne \pm 3\) ta được \(x > - 1\) và \(x \ne 3.\)
Vậy để \(\dfrac{A}{B} < {x^2} + 5\) thì \(x > - 1\) và \(x \ne 3.\)
Giải bất phương trình \(\dfrac{{x - 1}}{2} + \dfrac{{2 - x}}{3} \le \dfrac{{3x - 3}}{4}\) ta được tập nghiệm là:
-
A
\(S = \left\{ {x|x \ge \dfrac{{11}}{7}} \right\}\)
-
B
\(S = \left\{ {x|x \le \dfrac{{11}}{7}} \right\}\)
-
C
\(S = \left\{ {x|x > \dfrac{{11}}{7}} \right\}\)
-
D
\(S = \left\{ {x|x < \dfrac{{11}}{7}} \right\}\)
Đáp án của giáo viên lời giải hay : A
Biến đổi bất phương trình về dạng bất phương trình một ẩn và giải bất phương trình.
\(\begin{array}{l}\;\;\;\dfrac{{x - 1}}{2} + \dfrac{{2 - x}}{3} \le \dfrac{{3x - 3}}{4}\\ \Leftrightarrow \dfrac{{\left( {x - 1} \right).6}}{{2.6}} + \dfrac{{\left( {2 - x} \right).4}}{{3.4}} \le \dfrac{{\left( {3x - 3} \right).3}}{{4.3}}\\ \Leftrightarrow 6\left( {x - 1} \right) + 4\left( {2 - x} \right) \le 3\left( {3x - 3} \right)\\ \Leftrightarrow 6x - 6 + 8 - 4x \le 9x - 9\\ \Leftrightarrow 2x + 2 \le 9x - 9\\ \Leftrightarrow 9x - 2x \ge 2 + 9\\ \Leftrightarrow 7x \ge 11\\ \Leftrightarrow x \ge \dfrac{{11}}{7}\end{array}\)\(\).
Vậy tập nghiệm của bất phương trình là \(S = \left\{ {x|x \ge \dfrac{{11}}{7}} \right\}.\)
Lúc 6 giờ, ô tô thứ nhất khởi hành từ A. Đến 7 giờ 30 phút ô tô thứ hai cũng khởi hành từ A đuổi theo và kịp gặp ô tô thứ nhất lúc 10 giờ 30 phút. Biết vận tốc ô tô thứ hai lớn hơn vận tốc ô tô thứ nhất là 20km/h. Tính vận tốc ô tô thứ hai?
-
A
\(30\,km/h\)
-
B
\(50\,km/h\)
-
C
\(40\,km/h\)
-
D
\(60\,km/h\)
Đáp án của giáo viên lời giải hay : D
Bước 1. Lập phương trình:
Chọn ẩn số và đặt điều kiện thích hợp cho ẩn số;
Biểu diễn các đại lượng chưa biết theo ẩn và các đại lượng đã biết;
Lập phương trình biểu thị mối quan hệ giữa các đại lượng.
Bước 2. Giải phương trình.
Bước 3. Trả lời: Kiểm tra xem trong các nghiệm của phương trình, nghiệm nào thỏa mãn điều kiện của ẩn, nghiệm nào không, rồi kết luận.
Gọi vận tốc của ô tô thứ nhất là \(x\;\left( {km/h} \right), \left( {x > 0} \right)\).
\( \Rightarrow \) Vận tốc của ô tô thứ hai là \(x + 20 \left( {km/h} \right)\).
Đổi: 7 giờ 30 phút = 7,5h; 10 giờ 30 phút = 10,5h.
Thời gian ô tô thứ nhất đi đến khi gặp ô tô thứ hai là \(10,5 - 6 = 4,5\;h.\)
Thời gian ô tô thứ hai đi đến khi gặp ô tô thứ nhất là \(10,5 - 7,5 = 3\;h.\)
Theo bài ta có phương trình sau:
\(\begin{array}{l}\;\;\;4,5x = 3\left( {x + 20} \right)\\ \Leftrightarrow 4,5x = 3x + 60\\ \Leftrightarrow 1,5x = 60\\ \Leftrightarrow x = 40\;\left( {tm} \right)\end{array}\)
Vậy vận tốc ô tô thứ nhất là \(40km/h,\) vận tốc ô tô thứ hai là \(40 + 20 = 60\;km/h.\)
Cho \(\Delta ABC\) vuông tại A, đường cao AH. Kẻ đường phân giác AD của \(\Delta CHA\) và đường phân giác BK của \(\Delta ABC\;(D \in BC;\;K \in AC)\). BK cắt lần lượt AH và AD tại E và F.
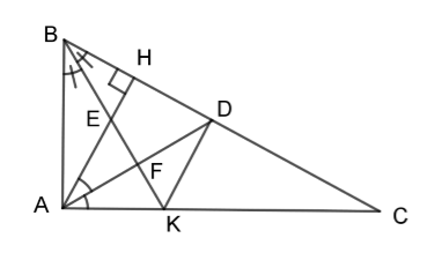
Chọn câu đúng.
-
A
\(\Delta AHB \backsim \Delta CAH\)
-
B
\(\Delta AHB \backsim \Delta CHA\)
-
C
\(\Delta AHB \backsim \Delta ADC\)
-
D
Cả A, B, C đều sai
Đáp án của giáo viên lời giải hay : B
Chứng minh cặp tam giác đồng dạng theo trường hợp góc – góc.
Xét \(\Delta AHB\) và \(\Delta CHA\) ta có:
\(\widehat {BHA} = \widehat {AHC} = {90^0}\;\left( {gt} \right)\)
\(\widehat {HAB} = \widehat {HCA}\) (cùng phụ góc \(HAC\))
\( \Rightarrow \Delta AHB \backsim \Delta CHA\; (g - g)\)
Chọn câu đúng.
-
A
\(\Delta AEF \backsim \Delta BHE\)
-
B
\(\Delta AEF \backsim \Delta BEH\)
-
C
\(\Delta AFE \backsim \Delta BEH\)
-
D
Cả A, B, C đều sai.
Đáp án của giáo viên lời giải hay : B
Áp dụng tính chất đường phân giác và kết quả câu trước để chứng minh cặp tam giác đồng dạng theo trường hợp góc – góc.
Vì \(\Delta AHB \backsim \Delta CHA\) (chứng minh câu trước) nên \(\widehat {HBA} = \widehat {HAC}\) (cặp góc tương ứng) (1)
Mà theo bài ra ta có:
\(\widehat {HBE} = \dfrac{1}{2}\widehat {HBA}\;\;\;(BK\) là phân giác của \(\widehat {ABC})\;\;\left( 2 \right)\)
\(\widehat {HAD} = \dfrac{1}{2}\widehat {HAC}\;\;(AD\) là phân giác của \(\widehat {HAC})\;\;\left( 3 \right)\)
Từ (1); (2); (3) ta có: \(\widehat {HBE} = \widehat {HAD} = \widehat {EAF}\)
Xét \(\Delta A{\rm{E}}F\) và \(\Delta BEH\) ta có:
\(\widehat {HBE} = \widehat {EAF}\;\;\left( {cmt} \right)\)
\(\widehat {HEB} = \widehat {FEA}\) (2 góc đối đỉnh)
\( \Rightarrow \Delta AEF \backsim \Delta BEH\;\;\left( {g - g} \right)\)
Chọn câu đúng nhất?
-
A
\(KD//AH\)
-
B
\(\dfrac{{EH}}{{AB}} = \dfrac{{KD}}{{BC}}\)
-
C
Cả A, B đều sai
-
D
Cả A, B đều đúng
Đáp án của giáo viên lời giải hay : D
+ Chứng minh tam giác cân, áp dụng tính chất tam giác cân để chứng minh 2 đường thẳng song song.
+ Chứng minh các cặp tam giác đồng dạng theo trường hợp góc – góc, sau đó áp dụng tính chất bắc cầu và tính chất của tam giác cân để chứng minh yêu cầu của đề bài.
*) Ta có: \(\Delta AEF \backsim \Delta BEH\) (theo câu trước)
\( \Rightarrow \widehat {AFE} = \widehat {BHE} = {90^0}\) (các góc tương ứng)
\( \Rightarrow BF \bot AD = \left\{ F \right\}.\)
Xét \(\Delta ABD\) ta có: \(BF\) vừa là đường cao đồng thời là đường phân giác của tam giác
\( \Rightarrow \Delta ABD\) là tam giác cân tại \(B \Rightarrow BF\) là đường phân giác của tam giác.
\( \Rightarrow F\) là trung điểm của \(AD\) hay \(AF = FD.\)
Xét \(\Delta AKD\) ta có: \(KF\) vừa là đường cao đồng thời là đường trung tuyến của tam giác
\( \Rightarrow \Delta AKD\) là tam giác cân tại \(K.\)
\( \Rightarrow \widehat {KAD} = \widehat {KDA}\) (hai góc kề đáy)
\( \Rightarrow \widehat {KAD} = \widehat {DAH}\;\left( { = \widehat {KAD}} \right)\)
Mà hai góc này là hai góc so le trong
\( \Rightarrow KD//AH.\)
*) Xét \(\Delta BHA\) và \(\Delta BAC\) ta có:
\(\begin{array}{l}\widehat B:\;chung\\\widehat {BHA} = \widehat {BAC} = {90^0}\;\left( {gt} \right)\\ \Rightarrow \Delta BHA \backsim \Delta BAC\;\left({g - g}\right)\end{array}\)
\( \Rightarrow \dfrac{{BH}}{{BA}} = \dfrac{{BA}}{{BC}}\) (các cặp cạnh tương ứng) (*)
Xét \(\Delta BHE\) và \(\Delta BAK\) ta có:
\(\begin{array}{l}\widehat {BHE} = \widehat {BAK} = {90^0}\;\;\left( {gt} \right)\\\widehat {HBE} = \widehat {ABK}\;\;\left( {gt} \right)\\ \Rightarrow \Delta BHE \backsim \Delta BAK\;\;\left( {g - g} \right)\end{array}\)
\( \Rightarrow \dfrac{{BH}}{{BA}} = \dfrac{{HE}}{{AK}}\) (các cặp cạnh tương ứng)
Mà \(\Delta AKD\) cân tại \(K\;\;\left( {cm\;c)} \right) \Rightarrow KA = KD\)
\( \Rightarrow \dfrac{{BH}}{{BA}} = \dfrac{{HE}}{{AK}} = \dfrac{{EH}}{{KD}}\) (**)
Từ (*) và (**) ta có: \(\dfrac{{EH}}{{KD}} = \dfrac{{BA}}{{BC}}\)\( \Leftrightarrow \dfrac{{EH}}{{AB}} = \dfrac{{KD}}{{BC}}\) (đpcm).
Cho $a,b,c$ là các số thực dương. Chọn câu đúng.
-
A
\(\dfrac{1}{a} + \dfrac{1}{b} + \dfrac{1}{c} \ge \dfrac{2}{{a + b}} + \dfrac{2}{{b + c}} + \dfrac{2}{{c + a}}\)
-
B
\(\dfrac{1}{a} + \dfrac{1}{b} + \dfrac{1}{c} \le \dfrac{2}{{a + b}} + \dfrac{2}{{b + c}} + \dfrac{2}{{c + a}}\)
-
C
\(\dfrac{1}{a} + \dfrac{1}{b} + \dfrac{1}{c} \ge \dfrac{3}{{a + b}} + \dfrac{3}{{b + c}} + \dfrac{3}{{c + a}}\)
-
D
\(\dfrac{1}{a} + \dfrac{1}{b} + \dfrac{1}{c} \ge \dfrac{2}{{a + b}} + \dfrac{3}{{b + c}} + \dfrac{2}{{c + a}}\)
Đáp án của giáo viên lời giải hay : A
Áp dụng BĐT \(\dfrac{1}{x} + \dfrac{1}{y} \ge \dfrac{4}{{x + y}}\) với \(x,y > 0.\) Dấu xảy ra khi \(x = y > 0\)
Ta chứng minh bất đẳng thức \(\dfrac{1}{x} + \dfrac{1}{y} \ge \dfrac{4}{{x + y}}\) với \(x,y > 0.\)
Ta có \(\dfrac{1}{x} + \dfrac{1}{y} \ge \dfrac{4}{{x + y}} \Leftrightarrow \dfrac{{x + y}}{{xy}} \ge \dfrac{4}{{x + y}}\)\( \Leftrightarrow {\left( {x + y} \right)^2} \ge 4xy \Leftrightarrow {x^2} - 2xy + {y^2} \ge 0\)\( \Leftrightarrow {\left( {x - y} \right)^2} \ge 0\) đúng với mọi \(x,y > 0.\)
Nên ta có \(\dfrac{1}{x} + \dfrac{1}{y} \ge \dfrac{4}{{x + y}}\) với \(x,y > 0.\)
Áp dụng bất đẳng thức trên, ta được:
\(\dfrac{1}{a} + \dfrac{1}{b} \ge \dfrac{4}{{a + b}}\) (1)
\(\dfrac{1}{b} + \dfrac{1}{c} \ge \dfrac{4}{{b + c}}\) (2)
\(\dfrac{1}{c} + \dfrac{1}{a} \ge \dfrac{4}{{c + a}}\) (3)
Cộng vế với vế của (1); (2); (3) ta có \(2\left( {\dfrac{1}{a} + \dfrac{1}{b} + \dfrac{1}{c}} \right) \ge 4\left( {\dfrac{1}{{a + b}} + \dfrac{1}{{b + c}} + \dfrac{1}{{c + a}}} \right)\)
\( \Leftrightarrow \dfrac{1}{a} + \dfrac{1}{b} + \dfrac{1}{c} \ge \dfrac{2}{{a + b}} + \dfrac{2}{{b + c}} + \dfrac{2}{{c + a}}\)
Dấu “ = ” xảy ra khi \(a = b = c > 0.\)
