Phân tích đa thức \({x^3} + x{}^2 - 4x - 4\) thành nhân tử ta được:
-
A
\((x - 2)(x + 2)(x + 1)\)
-
B
\((x - 4)(x + 4)(x + 1)\)
-
C
\((x - 2)(x + 2)(x - 1)\)
-
D
\(({x^2} + 4)(x + 1)\)
Đáp án của giáo viên lời giải hay : A
Phân tích đa thức thành nhân tử dựa vào các biện pháp: đặt nhân tử chung, dùng hằng đẳng thức,…
\(\begin{array}{l}\,\,{x^3} + x{}^2 - 4x - 4\\ = {x^2}(x + 1) - 4(x + 1)\\ = ({x^2} - 4)(x + 1)\\ = (x - 2)(x + 2)(x + 1)\end{array}\)
Căn bậc hai số học của 4 là:
-
A
\( - 2\)
-
B
\(2\)
-
C
\(16\)
-
D
\( \pm 2\)
Đáp án của giáo viên lời giải hay : B
Căn bậc hai số học của số \(a\) không âm là số \(x\) không âm sao cho \({x^2} = a.\)
Kí hiệu: \(x = \sqrt a .\)
Vì \({2^2} = 4\) và \(2 > 0\) nên \(\sqrt 4 = 2.\)
So sánh 5 với \(2\sqrt 6 \) ta có kết luận sau:
-
A
\(5 > 2\sqrt 6 \)
-
B
\(5 < 2\sqrt 6 \)
-
C
\(5 = 2\sqrt 6 \)
-
D
Không so sánh được
Đáp án của giáo viên lời giải hay : A
Với \(0 < a < b \Leftrightarrow \sqrt a < \sqrt b \)
Và với \(a,b > 0\) thì \({a^2} < {b^2} \Leftrightarrow a < b\).
Ta có: \({5^2} = 25;\,{\left( {2\sqrt 6 } \right)^2} = {2^2}.{\left( {\sqrt 6 } \right)^2} = 4.6 = 24\)
Vì \(25 > 24\) nên \(5 > 2\sqrt 6 .\)
\(\sqrt {{{\rm{x}}^2}} = 5\) thì \(x\) bằng:
-
A
\(25\)
-
B
\(5\)
-
C
\( \pm 5\)
-
D
\( \pm 25\)
Đáp án của giáo viên lời giải hay : C
Sử dụng \(\sqrt {{A^2}} = \left| A \right|\) và \(\left| x \right| = m\left( {m \ge 0} \right) \Leftrightarrow \left[ \begin{array}{l}x = m\\x = - m\end{array} \right.\)
Ta có: \(\sqrt {{{\rm{x}}^2}} = 5 \Leftrightarrow \left| x \right| = 5 \Leftrightarrow \left[ \begin{array}{l}x = 5\\x = - 5\end{array} \right.\)
Thực hiện phép tính sau \(\dfrac{{x - 3}}{{2x + 6}}:\left( {{x^2} - 6x + 9} \right)\), ta được kết quả là:
-
A
\(\dfrac{1}{{2({x^2} - 9)}}\)
-
B
\(\dfrac{1}{{{x^2} - 9}}\)
-
C
\(\dfrac{1}{{2{{(x - 3)}^2}}}\)
-
D
\(\dfrac{1}{{x - 9}}\)
Đáp án của giáo viên lời giải hay : A
Sử dụng kiến thức:
+) Áp dụng công thức của các hằng đẳng thức đáng nhớ.
+) Phân tích đa thức thành nhân tử.
+) Rút gọn phân thức.
Ta có: \(\dfrac{{x - 3}}{{2x + 6}}:\left( {{x^2} - 6x + 9} \right) = \dfrac{{x - 3}}{{2(x + 3)}}.\dfrac{1}{{{{(x - 3)}^2}}} = \dfrac{1}{{2(x - 3)(x + 3)}} = \dfrac{1}{{2({x^2} - 9)}}\).
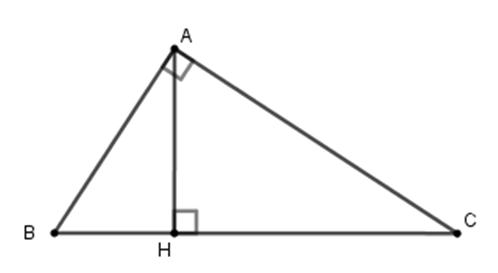
Nếu \(\Delta ABC\) vuông tại A có \(BH = 9,HC = 25\) thì đường cao \(AH\) có độ dài là:
-
A
\(15\)
-
B
\(225\)
-
C
\(\sqrt {15} \)
-
D
\(\dfrac{{25}}{9}\)
Đáp án của giáo viên lời giải hay : A
Sử dụng hệ thức lượng trong tam giác vuông: “Bình phương đường cao ứng với cạnh huyền bằng tích hai hình chiếu của hai cạnh góc vuông trên cạnh huyền”.
Xét tam giác \(ABC\) vuông tại \(A\) có chiều cao \(AH.\) Theo hệ thức lượng trong tam giác vuông ta có:
\(A{H^2} = HB.HC \Leftrightarrow A{H^2} = 9.25\) \( \Leftrightarrow A{H^2} = 225 \Rightarrow AH = 15\)
Vậy \(AH = 15\,cm.\)
Nghiệm của phương trình \(2x - 5 = 0\) là:
-
A
\(x = \dfrac{1}{5}\)
-
B
\(x = \dfrac{2}{5}\)
-
C
\(x = 2\)
-
D
\(x = \dfrac{5}{2}\)
Đáp án của giáo viên lời giải hay : D
Biến đổi phương trình về dạng phương trình bậc nhất một ẩn, giải phương trình bậc nhất một ẩn.
\(ax + b = 0 \Leftrightarrow ax = - b \Leftrightarrow x = \dfrac{{ - b}}{a}\;\left( {a \ne 0} \right)\).
Ta có: \(2x - 5 = 0 \Leftrightarrow 2x = 5\, \Leftrightarrow x = \dfrac{5}{2}\).
Có bao nhiêu giá trị của \(x\) thỏa mãn phương trình \(\left| {x - 3} \right| = 1 - 3x\).
-
A
\(3\)
-
B
\(0\)
-
C
\(1\)
-
D
\(2\)
Đáp án của giáo viên lời giải hay : C
Áp dụng định nghĩa giá trị tuyệt đối của một số hữu tỉ để tìm \(x:\left| x \right| = \left\{ \begin{array}{l}x\;\;khi\;\;\;x \ge 0\\ - x\;\;\;khi\;\;x < 0\end{array} \right.\)
Sau đó biến đổi phương trình, giải phương trình bậc nhất một ẩn.
\(\left| {x - 3} \right| = 1 - 3x \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x - 3 \ge 0\\x - 3 = 1 - 3x\end{array} \right.\\\left\{ \begin{array}{l}x - 3 < 0\\x - 3 = 3x - 1\end{array} \right.\end{array} \right.\)\( \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x \ge 3\\x + 3x = 1 + 3\end{array} \right.\\\left\{ \begin{array}{l}x < 3\\x - 3x = 3 - 1\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x \ge 3\\x = 1\end{array} \right.\\\left\{ \begin{array}{l}x < 3\\x = - 1\end{array} \right.\end{array} \right. \Leftrightarrow x = - 1\).
Vậy có 1 giá trị \(x\) thỏa mãn là \(x = - 1.\)
Tập nghiệm của bất phương trình \(5x + 1 < - 3\) là:
-
A
\(S = \left\{ {x|x > - \dfrac{4}{5}} \right\}\)
-
B
\(S = \left\{ {x|x < - \dfrac{4}{5}} \right\}\)
-
C
\(S = \left\{ {x|x < \dfrac{4}{5}} \right\}\)
-
D
\(S = \left\{ {x|x > \dfrac{4}{5}} \right\}\)
Đáp án của giáo viên lời giải hay : B
Biến đổi bất phương trình về dạng bất phương trình một ẩn và giải bất phương trình.
\(5x + 1 < - 3 \Leftrightarrow 5x < - 3 - 1\) \( \Leftrightarrow x < \dfrac{{ - 4}}{5}\).
Tập nghiệm của bất phương trình là \(S = \left\{ {x|x < - \dfrac{4}{5}} \right\}\).
Chọn câu đúng. Giá trị của phân thức \(\dfrac{{{x^2} - x}}{{2(x - 1)}}\) tại \(x = 4\) là:
-
A
\(4\)
-
B
\(2\)
-
C
\(6\)
-
D
\(8\)
Đáp án của giáo viên lời giải hay : B
Phân tích các mẫu thức thành nhân tử.
Rút gọn biểu thức và tính giá trị biểu thức.
Đk: \(x - 1 \ne 0 \Leftrightarrow x \ne 1.\)
\(A = \dfrac{{{x^2} - x}}{{2(x - 1)}} = \dfrac{{x(x - 1)}}{{2(x - 1)}} = \dfrac{x}{2} (x \ne 1)\).
Với \(x = 4\) (tmđk) ta thay \(x = 4\) vào A ta được: \(A = \dfrac{4}{2} = 2.\)
Với điều kiện nào của \(x\) thì \(\dfrac{{x - 2}}{{3 + 2x}} \le 0\).
-
A
\( - \dfrac{3}{2} \le x \le 2\)
-
B
\( - \dfrac{3}{2} < x < 2\)
-
C
\( - \dfrac{3}{2} < x \le 2\)
-
D
\(x \le 2\)
Đáp án của giáo viên lời giải hay : C
Sử dụng: \(\dfrac{A}{B} \le 0 \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}A \le 0\\B > 0\end{array} \right.\\\left\{ \begin{array}{l}A \ge 0\\B < 0\end{array} \right.\end{array} \right.\)
Rồi giải từng bất phương trình bậc nhất một ẩn thu được.
\(\dfrac{{x - 2}}{{3 + 2x}} \le 0 \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x - 2 \ge 0\\3 + 2x < 0\end{array} \right.\\\left\{ \begin{array}{l}x - 2 \le 0\\3 + 2x > 0\end{array} \right.\end{array} \right.\)\( \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x - 2 \ge 0\\3 + 2x < 0\end{array} \right.\\\left\{ \begin{array}{l}x - 2 \le 0\\3 + 2x > 0\end{array} \right.\end{array} \right.\)\( \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x \ge 2\\x < \dfrac{{ - 3}}{2}\end{array} \right.\\\left\{ \begin{array}{l}x \le 2\\x > \dfrac{{ - 3}}{2}\end{array} \right.\end{array} \right. \Leftrightarrow \dfrac{{ - 3}}{2} < x \le 2\).
Vậy \( - \dfrac{3}{2} < x \le 2.\)
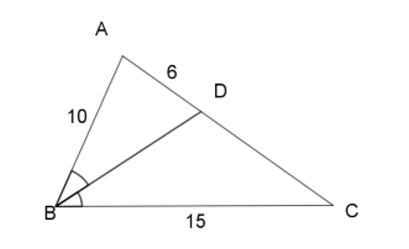
Cho \(\Delta ABC\), đường phân giác góc \(B\) cắt \(AC\) tại \(D\) và cho biết \(AB = 10{\rm{ }}cm,{\rm{ }}BC = 15{\rm{ }}cm,\)\(AD = 6{\rm{ }}cm.\) Tính \(AC.\)
-
A
\(6{\rm{ }}cm\)
-
B
\(9{\rm{ }}cm\)
-
C
\(12{\rm{ }}cm\)
-
D
\(15{\rm{ }}cm\)
Đáp án của giáo viên lời giải hay : D
Áp dụng tính chất đường phân giác của tam giác để tính \(AC.\)
Áp dụng tính chất đường phân giác trong tam giác ABC, ta có: \(\dfrac{{BA}}{{AD}} = \dfrac{{BC}}{{CD}}\)
\( \Rightarrow \dfrac{{10}}{6} = \dfrac{{15}}{{CD}} \Leftrightarrow CD = \dfrac{{6.15}}{{10}} = 9\;cm\)
\( \Rightarrow AC = AD + DC = 6 + 9 = 15\;cm\).
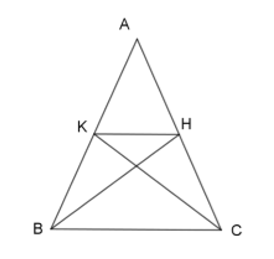
Cho tam giác \(ABC\) có \(AB = AC;{\rm{ }}BC = 8{\rm{ }}cm;\) \(BH\) và \(CK\) là hai đường trung tuyến kẻ từ \(B\) và \(C.\) Tính độ dài đoạn \(HK.\)
-
A
\(HK = 2\;cm\)
-
B
\(HK = 4\;cm\)
-
C
\(HK = 6\;cm\)
-
D
\(HK = 8\;cm\)
Đáp án của giáo viên lời giải hay : B
Áp dụng lý thuyết đã học và cách chứng minh tam giác đồng dạng để thực hiện yêu cầu của bài toán.
Theo bài ra ta có: \(AB = AC\) (1)
Ta lại có $BH$ và $CK$ là hai đường trung tuyến kẻ từ $B$ và $C$ của tam giác $ABC,$ suy ra $H$ và $K$ lần lượt là trung điểm của $AC$ và $AB.$
Khi đó, ta có:
\(AK = KB = \dfrac{1}{2}AB\;(2)\)
\(AH = HC = \dfrac{1}{2}AC\;(3)\)
Từ (1), (2) và (3) ta có: \(AK = AH\)
Vì $AK = AH$ và $AB = AC$ nên: \(\dfrac{{AK}}{{AB}} = \dfrac{{AH}}{{AC}}\)
Xét \(\Delta AKH\) và \(\Delta ABC\) ta có:
+) \(\dfrac{{AK}}{{AB}} = \dfrac{{AH}}{{AC}}\)
+) \(\widehat A\) chung
\( \Rightarrow \Delta AKH \backsim \Delta ABC\; (c - g - c)\)
\(\begin{array}{l} \Rightarrow \dfrac{{AK}}{{AB}} = \dfrac{{KH}}{{BC}} = \dfrac{1}{2}\\ \Rightarrow \dfrac{{KH}}{8} = \dfrac{1}{2} \Leftrightarrow KH = \dfrac{8}{2} = 4\;cm\end{array}\).
Giải phương trình \(\dfrac{{x - 1}}{{x + 2}} - \dfrac{{1 - x}}{{2 - x}} = \dfrac{{2({x^2} + 2)}}{{{x^2} - 4}}\) ta được tập nghiệm là:
-
A
\(S = \left\{ 0 \right\}\)
-
B
\(S = \left\{ {0; - 2} \right\}\)
-
C
\(S = \left\{ {0;2} \right\}\)
-
D
\(S = \left\{ { - 2} \right\}\)
Đáp án của giáo viên lời giải hay : A
Giải phương trình chứa ẩn ở mẫu:
Bước 1: Tìm điều kiện xác định của phương trình.
Bước 2: Quy đồng mẫu hai vế của phương trình rồi khử mẫu.
Bước 3: Giải phương trình vừa nhận được.
Bước 4: (Kết luận) Trong các giá trị của ẩn tìm được ở bước 3, các giá trị thỏa mãn điều kiện xác định chính là các nghiệm của phương trình đã cho.
ĐKXĐ: \(x \ne 2;\,\,x \ne - 2\)
\(\begin{array}{l}\,\,\,\,\,\,\,\dfrac{{x - 1}}{{x + 2}} - \dfrac{{1 - x}}{{2 - x}} = \dfrac{{2({x^2} + 2)}}{{{x^2} - 4}}\\ \Leftrightarrow \dfrac{{x - 1}}{{x + 2}} + \dfrac{{1 - x}}{{x - 2}} = \dfrac{{2({x^2} + 2)}}{{(x - 2)(x + 2)}}\\ \Leftrightarrow \dfrac{{(x - 1)(x - 2)}}{{(x - 2)(x + 2)}} + \dfrac{{(1 - x)(x + 2)}}{{(x - 2)(x + 2)}} = \dfrac{{2({x^2} + 2)}}{{(x - 2)(x + 2)}}\\ \Rightarrow (x - 1)(x - 2) + (1 - x)(x + 2) = 2({x^2} + 2)\\ \Leftrightarrow {x^2} - 2x - x + 2 + x + 2 - {x^2} - 2x = 2{x^2} + 4\\ \Leftrightarrow 2{x^2} + 4x = 0\\ \Leftrightarrow 2x(x + 2) = 0\\ \Leftrightarrow \left[ \begin{array}{l}2x = 0\\x + 2 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0\,\,\,\,\,(TM)\\x = - 2\,\,\,\,\,(KTM)\end{array} \right.\end{array}\)
Vậy tập nghiệm của phương trình là \(S = \left\{ 0 \right\}.\)
Để chuẩn bị cho năm học mới, bạn Nam đã mua tất cả \(26\) quyển vở gồm loại \(200\) trang và loại \(120\) trang. Mỗi quyển vở loại \(200\) trang có giá \(13500\) đồng, mỗi quyển vở loại \(120\) trang có giá \(9500\) đồng. Bạn Nam đã trả số tiền là \(263000\) đồng.
Tính số vở loại \(120\) trang mà bạn Nam đã mua?
-
A
\(24\) quyển
-
B
\(20\) quyển
-
C
\(4\) quyển
-
D
\(22\) quyển
Đáp án của giáo viên lời giải hay : D
Bước 1. Lập phương trình:
Chọn ẩn số và đặt điều kiện thích hợp cho ẩn số;
Biểu diễn các đại lượng chưa biết theo ẩn và các đại lượng đã biết;
Lập phương trình biểu thị mối quan hệ giữa các đại lượng.
Bước 2. Giải phương trình.
Bước 3. Trả lời: Kiểm tra xem trong các nghiệm của phương trình, nghiệm nào thỏa mãn điều kiện của ẩn, nghiệm nào không, rồi kết luận.
Gọi số quyển vở loại 200 trang bạn Nam mua là x (quyển, điều kiện \(x \in {\mathbb{N}^*},{\rm{ }}x < 26\) ) thì số quyển vở loại 120 trang là: \(26-x\) ( quyển)
Số tiền mua vở loại 200 trang là: \(13500x\) (đồng)
Số tiền mua vở loại 120 trang là: \(9500\left( {26 - x} \right)\) (đồng)
Vì bạn Nam đã trả tổng số tiền là \(263000\) đồng nên ta có phương trình \(13500x + 9500(26 - x) = 263000\)
\( \Leftrightarrow 13500x - 9500x = 263000 - 9500. 26\).
\( \Leftrightarrow 4000x = 16000\)\( \Leftrightarrow x = 4\) (thỏa mãn)
Vậy bạn Nam mua 4 quyển vở loại 200 trang, 22 quyển vở loại 120 trang.
Nhân dịp đầu năm học mới, nhà sách thực hiện chương trình giảm giá cho học sinh học sinh giỏi như sau: mỗi quyển loại 200 trang được giảm 5% còn mỗi quyển loại 120 trang được giảm 10%. Nếu năm học trước bạn Nam đạt danh hiệu học sinh giỏi thì bạn chỉ phải trả bao nhiêu tiền cho số vở trên.
-
A
\(236400\) đồng
-
B
\(239400\) đồng
-
C
\(240400\) đồng
-
D
\(239600\) đồng
Đáp án của giáo viên lời giải hay : B
Sử dụng kết quả câu trước bạn Nam mua 4 quyển vở loại 200 trang, 22 quyển vở loại 120 trang.
Từ đó tính số tiền Nam phải trả sau khi được giảm giá.
Số tiền Nam được giảm khi mua 4 quyển vở loại 200 trang, 22 quyển vở loại 120 trang là:
\(13500. 4. 5\% {\rm{ }} + {\rm{ }}9500. 22. 10\% = 23600\) đồng.
Số tiền bạn phải trả nếu được giảm giá là:
\(263000--23600 = 239400\) (đồng).
Cho \(\Delta ABC\) có \(\widehat A\, = \,{90^0}\), \(AB = 2cm,AC = 6cm.\) Trên cạnh \(AC\) lấy điểm \(E,{\rm{ }}K\) sao cho \(AE = 2cm\) và \(K\) là trung điểm của đoạn thẳng \(EC.\)
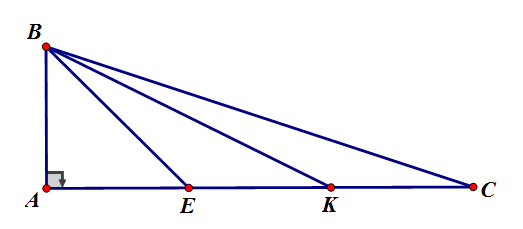
Tính \(BE\) và các tỉ số \(\dfrac{{BE}}{{EK}};\) \(\dfrac{{CE}}{{EB}}\).
-
A
\(BE = 2\sqrt 2 \,cm;\dfrac{{BE}}{{EK}} = 2;\dfrac{{CE}}{{EB}} = 2\)
-
B
\(BE = 2\sqrt 2 \,cm;\dfrac{{BE}}{{EK}} = 2\sqrt 2 ;\dfrac{{CE}}{{EB}} = \dfrac{{\sqrt 2 }}{2}\)
-
C
\(BE = 2\sqrt 2 \,cm;\dfrac{{BE}}{{EK}} = \sqrt 2 ;\dfrac{{CE}}{{EB}} = \sqrt 2 \)
-
D
\(BE = \sqrt 2 \,cm;\dfrac{{BE}}{{EK}} = \sqrt 2 ;\dfrac{{CE}}{{EB}} = \sqrt 2 \)
Đáp án của giáo viên lời giải hay : C
Áp dụng định lí Pitago để tính độ dài cạnh \(BE\). Từ đó tính các tỉ số.
Vì \(AE = 2cm;AC = 6cm \Rightarrow EC = 4cm\)
Lại có \(K\) là trung điểm \(EC\) nên \(EK = KC = \dfrac{{EC}}{2} = 2cm\)
Ta có: \(AE = EK = KC = {\rm{ }}2cm\)
Xét tam giác \(ABE\) vuông tại \(A.\) Theo định lý Pytago ta có \(B{E^2} = A{B^2} + A{E^2}\)\( = {2^2} + {2^2} = 8\).
Suy ra: \(BE = 2\sqrt 2 \,cm\).
Từ đó suy ra: \(\dfrac{{BE}}{{EK}} = \dfrac{{2\sqrt 2 }}{2} = \sqrt 2 \) và \(\dfrac{{CE}}{{EB}} = \dfrac{4}{{2\sqrt 2 }} = \sqrt 2 \).
Chọn câu đúng.
-
A
\(\Delta BEK \backsim \Delta CEA\)
-
B
\(\Delta BEK \backsim \Delta CBE\)
-
C
\(\Delta BEK \backsim \Delta CEB\)
-
D
\(\Delta BEK \backsim \Delta ECB\)
Đáp án của giáo viên lời giải hay : C
Chứng minh 2 tam giác đồng dạng theo trường hợp cạnh - góc – cạnh.
Từ câu trước ta có: \(\dfrac{{BE}}{{EK}} = \sqrt 2 ;\dfrac{{CE}}{{EB}} = \sqrt 2 \) suy ra: \(\dfrac{{BE}}{{EK}} = \dfrac{{CE}}{{EB}}\)
Xét tam giác \(\Delta BEK\)và \(\Delta CEB\) có:
+) \(\dfrac{{BE}}{{EK}} = \dfrac{{CE}}{{EB}}\)
+) \(\widehat {CEB}\) chung
Suy ra: \(\Delta BEK \backsim \Delta CEB\) (c – g - c)
Tính \(\widehat {BKE} + \widehat {BCE}\).
-
A
\({120^0}\)
-
B
\({30^0}\)
-
C
\({45^0}\)
-
D
\({60^0}\)
Đáp án của giáo viên lời giải hay : C
Sử dụng kết quả câu trước \(\Delta BEK \backsim \Delta CEB\).
Sử dụng: Góc ngoài của tam giác tại một đỉnh bằng tổng hai góc trong không kề với đỉnh đó.
Tam giác \(EBA\) vuông cân tại \(A\) nên \(\widehat {BEA} = {45^0}.\)
Từ câu trước ta có: \(\Delta BEK \backsim \Delta CEB\)
Suy ra: \(\widehat {BKE} = \widehat {CBE}\)
Do đó: \(\widehat {BKE} + \widehat {BCE} = \widehat {CBE} + \widehat {BCE}\)
Ta lại có: \(\widehat {BEA}\)là góc ngoài của tam giác \(EBC\) nên \(\widehat {CBE} + \widehat {BCE} = \widehat {BEA} = {45^0}\)
Nên \(\widehat {BKE} + \widehat {BCE} = {45^0}.\)
Cho các số thực dương \(x,{\rm{ }}y,{\rm{ }}z\) thỏa mãn: \(\dfrac{1}{x} + \dfrac{1}{y} + \dfrac{1}{z} = 4\). Tìm giá trị lớn nhất của biểu thức \(P = \dfrac{1}{{2x + y + z}} + \dfrac{1}{{2y + x + z}} + \dfrac{1}{{2z + x + y}}\).
-
A
\(P = 4\)
-
B
\(P = 2\)
-
C
\(P = 1\)
-
D
\(P = \dfrac{3}{2}\)
Đáp án của giáo viên lời giải hay : C
Sử dụng bổ đề: Với \(x,y\) dương là hai số bất kỳ thì: \(\dfrac{1}{x} + \dfrac{1}{y} \ge \dfrac{4}{{x + y}}\).
Bổ đề: Với x,y dương là hai số bất kỳ thì: \(\dfrac{1}{x} + \dfrac{1}{y} \ge \dfrac{4}{{x + y}}\).
Chứng minh: Vì x, y dương nên \(\dfrac{1}{x} + \dfrac{1}{y} \ge \dfrac{4}{{x + y}} \Leftrightarrow {(x + y)^2} \ge 4xy\)
\( \Leftrightarrow {\left( {x - y} \right)^2} \ge 0\) với mọi x, y thỏa mãn yêu cầu.
Áp dụng bổ đề trên ta có: \(\dfrac{4}{{2x + y + z}} = \dfrac{4}{{\left( {x + y} \right) + \left( {x + z} \right)}} \le \dfrac{1}{{x + y}} + \dfrac{1}{{x + z}}\).
Cũng có: \(\dfrac{1}{{x + y}} + \dfrac{1}{{x + z}} \le \dfrac{1}{4}\left( {\dfrac{1}{x} + \dfrac{1}{y} + \dfrac{1}{x} + \dfrac{1}{z}} \right) = \dfrac{1}{4}\left( {\dfrac{2}{x} + \dfrac{1}{y} + \dfrac{1}{z}} \right)\).
Do đó: \(\dfrac{1}{{2x + y + z}} \le \dfrac{1}{{16}}\left( {\dfrac{2}{x} + \dfrac{1}{y} + \dfrac{1}{z}} \right)\).
Tương tự ta có:
\(\dfrac{1}{{x + 2y + z}} \le \dfrac{1}{{16}}\left( {\dfrac{1}{x} + \dfrac{2}{y} + \dfrac{1}{z}} \right)\)
\(\)
\(\dfrac{1}{{x + y + 2z}} \le \dfrac{1}{{16}}\left( {\dfrac{1}{x} + \dfrac{1}{y} + \dfrac{2}{z}} \right)\).
Cộng vế với vế các bất đẳng thức trên kết hợp với điều kiện \(\dfrac{1}{x} + \dfrac{1}{y} + \dfrac{1}{z} = 4\) ta có:
\(P = \dfrac{1}{{2x + y + z}} + \dfrac{1}{{2y + x + z}} + \dfrac{1}{{2z + x + y}}\)\( \le \dfrac{1}{{16}}\left( {\dfrac{2}{x} + \dfrac{1}{y} + \dfrac{1}{z} + \dfrac{1}{x} + \dfrac{2}{y} + \dfrac{1}{z} + \dfrac{1}{x} + \dfrac{1}{y} + \dfrac{2}{z}} \right)\)
\(P \le \dfrac{1}{{16}}\left( {\dfrac{4}{x} + \dfrac{4}{y} + \dfrac{4}{z}} \right) = \dfrac{1}{{16}}.4\left( {\dfrac{1}{x} + \dfrac{1}{y} + \dfrac{1}{z}} \right)\)\( = \dfrac{1}{4}.4 = 1\).
Hay \(\dfrac{1}{{2x + y + z}} + \dfrac{1}{{2y + x + z}} + \dfrac{1}{{2z + x + y}} \le 1\).
Dấu “=” xảy ra khi \(\left\{ \begin{array}{l}x + y = x + z\\x + y = y + z\\x + z = y + z\\\dfrac{1}{x} + \dfrac{1}{y} + \dfrac{1}{z} = 4\end{array} \right.\)\( \Leftrightarrow x = y = z = \dfrac{3}{4}\).
Vậy giá trị lớn nhất của \(P = \dfrac{1}{{2x + y + z}} + \dfrac{1}{{2y + x + z}} + \dfrac{1}{{2z + x + y}}\) là \(1.\)
