Bậc của đa thức \(f\left( x \right) = - 7{x^4} + 4{x^3} + 8{x^2} - 5{x^3} - {x^4} + 5{x^3} + 4{x^4} + 2020\) là:
-
A
\(2018\)
-
B
\(5\)
-
C
\(4\)
-
D
\(3\)
Đáp án của giáo viên lời giải hay : C
Thu gọn đa thức, rồi xác định bậc của đa thức đó. Bậc của đa thức là bậc của hạng tử có số mũ cao nhất trong dạng thu gọn của đa thức đó.
Ta có:
\(f\left( x \right) = - 7{x^4} + 4{x^3} + 8{x^2} - 5{x^3} - {x^4} + 5{x^3} + 4{x^4} + 2020\)\(= \left( { - 7{x^4} - {x^4} + 4{x^4}} \right) + \left( {4{x^3} - 5{x^3} + 5{x^3}} \right) + 8{x^2} + 2020\)\( = - 4{x^4} + 4{x^3} + 8{x^2} + 2018\)
\( \Rightarrow \) Bậc của đa thức \(f\left( x \right)\) là: \(4.\)
Cho bảng tần số:

Mốt của dấu hiệu là:
-
A
\(20\)
-
B
\(8\)
-
C
\(35\)
-
D
\(30\)
Đáp án của giáo viên lời giải hay : D
Mốt là giá trị có tần số lớn nhất, từ đó tìm đúng mốt.
Giá trị 30 có tần số lớn nhất là 10.
Suy ra 30 là mốt của dấu hiệu. Hay \({M_0} = 30\).
Nếu \(AM\) là đường trung tuyến và \(G\) là trọng tâm của tam giác \(ABC\) thì:
-
A
\(AM = AB\)
-
B
\(AG = \dfrac{2}{3}AM\)
-
C
\(AG = \dfrac{3}{4}AB\)
-
D
\(AM = AG\)
Đáp án của giáo viên lời giải hay : B
Định lý ba đường trung tuyến của một tam giác: Ba đường trung tuyến của một tam giác cùng đi qua một điểm. Điểm đó cách đều mỗi đỉnh một khoảng bằng \(\dfrac{2}{3}\) độ dài đường trung tuyến đi qua đỉnh ấy.
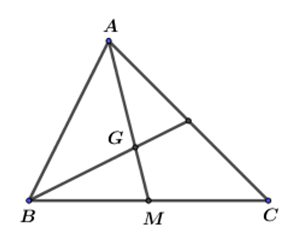
Dựa vào định lý ba đường trung tuyến của tam giác ABC.
Ta có: \(AG = \dfrac{2}{3}AM\).
Độ dài hai cạnh góc vuông liên tiếp lần lượt là \(5cm\) và \(12cm\) thì độ dài cạnh huyền là:
-
A
\(13\)
-
B
\(14\)
-
C
\(6\)
-
D
\(15\)
Đáp án của giáo viên lời giải hay : A
Sử dụng định lý py-ta-go: Trong một tam giác vuông bình phương cạnh huyền bằng bình phương hai cạnh góc vuông. Từ đó tính được cạnh huyền của tam giác khi biết hai cạnh góc vuông.
Ta có: \({5^2} + {12^2} = {13^2} \Rightarrow \) cạnh huyền bằng 13cm.
Số nào sau đây là nghiệm của đa thức \(A\left( x \right) = 3x - 2\).
-
A
\(0\)
-
B
\( - 2\)
-
C
\(\dfrac{2}{3}\)
-
D
\( - \dfrac{2}{3}\)
Đáp án của giáo viên lời giải hay : C
Giá trị của \(x\) làm cho \(A\left( x \right) = 0\) thì là nghiệm của đa thức đó.
Ta có:
\(\begin{array}{l}A\left( x \right) = 3x - 2 = 0\\ \Leftrightarrow \,3x = 2\\ \Leftrightarrow x = \dfrac{2}{3}\end{array}\).
Đơn thức thích hợp điền vào chỗ trống (…) trong phép toán: \(4{x^3} + ... = - 5{x^3}\) là:
-
A
\(6{x^3}\)
-
B
\(- 9{x^3}\)
-
C
\(0\)
-
D
\(9{x^3}\)
Đáp án của giáo viên lời giải hay : B
Chuyển vế đổi dấu các hạng tử, để tìm hạng tử chưa biết điền vào (…)
Ta có: \(4{x^2} + ... = - 5{x^3}\)\( \Rightarrow \) Đơn thức cần tìm là: \( - 5{x^3} - 4{x^3} = - 9{x^3}\).
Đơn thức nào sau đây đồng dạng với đơn thức \( - 3x{y^2}\).
-
A
\( - 3{x^2}y\)
-
B
\(\left( { - 8xy}\right)y\)
-
C
\( - 3{\left( {xy} \right)^2}\)
-
D
\( - 3xy\)
Đáp án của giáo viên lời giải hay : B
Hai đơn thức đồng dạng là hai đơn thức có cùng phần biến, nhưng khác hệ số.
Đơn thức khác hệ số và có cùng phần biến với đơn thức \( - 3x{y^2}\) là: \(\left( { - 8xy} \right)y = - 8x{y^2}\).
Kết quả của phép tính \( - 5{x^2}{y^5} - {x^2}{y^5} + 3{x^2}{y^5}\).
-
A
\( - 3{x^2}{y^5}\)
-
B
\(8{x^2}{y^5}\)
-
C
\(4{x^2}{y^5}\)
-
D
\( - 4{x^2}{y^5}\)
Đáp án của giáo viên lời giải hay : A
Cộng các đơn thức đồng dạng, ta cộng phần hệ số với nhau và giữ nguyên phần biến.
Ta có: \( - 5{x^2}{y^5} - {x^2}{y^5} + 3{x^2}{y^5} = \left( { - 5 - 1 + 3} \right){x^2}{y^5} = - 3{x^2}{y^5}\).
Giá trị của biểu thức \(3{x^2}y + 3{x^2}y\) tại \(x = - 2\) và \(y = - 1\) là:
-
A
\(12\)
-
B
\( - 9\)
-
C
\(18\)
-
D
\( - 24\)
Đáp án của giáo viên lời giải hay : D
Thu gọn đa thức rồi thay giá trị của x, y vào.
Thu gọn đa thức ta được: \(3{x^2}y + 3{x^2}y = 6{x^2}y\).
Thay \(x = - 2;\,y = - 1\) vào biểu thức đã được thu gọn ta có: \(6.{\left( { - 2} \right)^2}\left( { - 1} \right) = - 24\).
Đa thức \(g\left( x \right) = {x^2} + 2\).
-
A
Không có nghiệm
-
B
Có nghiệm là \( - 2\)
-
C
Có nghệm là \(2\)
-
D
Có 2 nghiệm
Đáp án của giáo viên lời giải hay : A
Đa thức không có nghiệm là không có giá trị nào của x làm cho đa thức bằng 0.
Ta thấy: \(g\left( x \right) = {x^2} + 2\) luôn luôn lớn hơn 0 nên đa thức không có nghiệm.
Tam giác có một góc \({60^0}\) thì với điều kiện nào thì trở thành tam giác đều:
-
A
Ba góc nhọn
-
B
Hai cạnh bằng nhau
-
C
Hai góc nhọn
-
D
Một cạnh đáy
Đáp án của giáo viên lời giải hay : B
Ta có: Tam giác cân có 1 góc bằng \({60^0}\) là tam giác đều.
Tam giác có một góc bằng \({60^0}\) và có hai cạnh bằng nhau là tam giác đều.
Cho tam giác \(ABC\) có \(\widehat C = {40^0};\,\widehat B = {60^0}.\) Câu nào sau đây đúng?
-
A
\(AB > AC > BC\)
-
B
\(AB > BC > AC\)
-
C
\(BC > AC > AB\)
-
D
\(AC > BC > AB\)
Đáp án của giáo viên lời giải hay : C
Sử dụng mối quan hệ giữa góc và cạnh của một tam giác.
Lưu ý: Trong một tam giác cạnh đối diện với góc lớn hơn là cạnh lớn hơn.
Tam giác \(ABC\) có: \(\widehat C = {40^0};\,\widehat B = {60^0}.\)
\( \Rightarrow \) \(\widehat A = {180^0} - \left( {{{40}^0} + {{60}^0}} \right) = {80^0}\)
Trong một tam giác cạnh đối diện với góc lớn hơn thì lớn hơn.
Ta có:
\(\begin{array}{l}\widehat A > \widehat B > \widehat C\,\,\left( {{{80}^0} > {{60}^0} > {{40}^0}} \right)\\ \Rightarrow BC > AC > AB\end{array}\).
Tính \(\dfrac{3}{4}. 26\dfrac{1}{5} - \dfrac{3}{4}. 44\dfrac{1}{5}\).
-
A
\(\dfrac{{27}}{2}\)
-
B
\( - \dfrac{{27}}{2}\)
-
C
\(13\)
-
D
\(14\)
Đáp án của giáo viên lời giải hay : B
Sử dụng tính chất \(A.B + A.C = A\left( {B + C} \right)\).
Ta có:
\(\begin{array}{l}\dfrac{3}{4}. 26\dfrac{1}{5} - \dfrac{3}{4}. 44\dfrac{1}{5}\\ = \dfrac{3}{4}\left( {26\dfrac{1}{5} - 44\dfrac{1}{5}} \right)\\ = \dfrac{3}{4} \cdot \left( { - 18} \right) = \dfrac{{ - 27}}{2}\end{array}\).
Biết độ dài các cạnh của một tam giác tỉ lệ với \(3,5,7.\) Tính độ dài cạnh lớn nhất của tam giác đó. Biết rằng cạnh lớn nhất dài hơn cạnh nhỏ nhất là \(8{\rm{ }}cm.\)
-
A
\(6\,cm\)
-
B
\(14\,cm\)
-
C
\(10\,cm\)
-
D
\(16\,cm\)
Đáp án của giáo viên lời giải hay : B
Sử dụng tính chất dãy tỉ số bằng nhau \(\dfrac{a}{b} = \dfrac{c}{d} = \dfrac{{a - c}}{{b - d}}\).
Gọi độ dài các cạnh của tam giác theo thứ tự tăng dần lần lượt là: \(a,b,c{\rm{ }}\left( {a,b,c > 0} \right)\)
Theo bài ra ta có: \(\dfrac{a}{3} = \dfrac{b}{5} = \dfrac{c}{7}\) và \(c - a = 8.\)
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\(\dfrac{a}{3} = \dfrac{b}{5} = \dfrac{c}{7}\)=\(\dfrac{{c - a}}{{7 - 3}} = \dfrac{8}{4} = 2\).
+) \(a = 2. 3 = 6\)
+) \(b = 2. 5 = 10\)
+) \(c = 2. 7 = 14\)
Vậy: độ dài các cạnh của tam giác lần lượt là: \(6{\rm{ }}cm;10{\rm{ }}cm;14cm.\)
Cho đa thức \(A\left( x \right) = {x^4} - {x^2} + 1\).
Tìm bậc của đa thức trên.
-
A
\(3\)
-
B
\(1\)
-
C
\(2\)
-
D
\(4\)
Đáp án của giáo viên lời giải hay : D
Bậc của đa thức là bậc của hạng tử có bậc cao nhất, trong dạng thu gọn của đa thức đó. Từ đó xác định bậc của đa thức đã cho.
\(A\left( x \right)\) có bậc 4.
Tính \(A\left( { - 1} \right);A\left( { - 2} \right).\)
-
A
\(A\left( { - 1} \right) = 1;A\left( { - 2} \right) = 13\)
-
B
\(A\left( { - 1} \right) = - 1;A\left( { - 2} \right) = - 13\)
-
C
\(A\left( { - 1} \right) = 1;A\left( { - 2} \right) = - 13\)
-
D
\(A\left( { - 1} \right) = - 1;A\left( { - 2} \right) = 13\)
Đáp án của giáo viên lời giải hay : A
Thay các giá trị \(x = - 1;x = - 2\) vào biểu thức của A để tính.
Ta có :
\(\begin{array}{l}A\left( { - 1} \right) = {\left( { - 1} \right)^4} - {\left( { - 1} \right)^2} + 1 = 1\\A\left( { - 2} \right) = \,{\left( { - 2} \right)^4} - {\left( { - 2} \right)^2} + 1 = 13\end{array}\).
Tìm nghiệm của đa thức \(Q\left( x \right) = 2{x^2} + x\).
-
A
\(x = 0;\,x = - \dfrac{1}{2}\)
-
B
\(x = 0;\,x = \dfrac{1}{2}\)
-
C
\(x = 0\)
-
D
\(x = \dfrac{1}{2}\)
Đáp án của giáo viên lời giải hay : A
Nghiệm của đa thức: Nếu tại \(x = a\) đa thức \(P\left( x \right)\) có giá trị bằng 0 thì ta nói \(a\) hoặc \(x = a\) là nghiệm của đa thức đó.
Ta cho biểu thức \(Q\left( x \right) = 0\) để tìm ra các giá trị của x làm cho \(Q\left( x \right) = 0\) (tìm nghiệm).
Ta có:
\(\begin{array}{l}2{x^2} + x = 0\\x\left( {2x + 1} \right) = 0\end{array}\)
\( \Rightarrow x = 0\) hoặc \(x = - \dfrac{1}{2}\)
Vậy \(Q\left( x \right)\) có nghiệm là \(x = 0;\,x = - \dfrac{1}{2}\).
Cho tam giác \(ABC\) cân tại \(A\) và hai đường trung tuyến \(BM,\,CN\) cắt nhau tại \(K\).
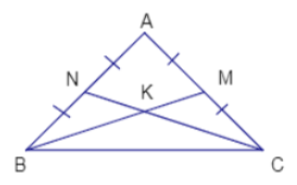
Chọn câu đúng.
-
A
\(\Delta BNC = \Delta CMB\)
-
B
\(\Delta BNC = \Delta CBM\)
-
C
\(\Delta BNC = \Delta MCB\)
-
D
\(\Delta BCN = \Delta CMB\)
Đáp án của giáo viên lời giải hay : A
Chứng minh hai tam giác bằng nhau theo trường hợp cạnh-góc-cạnh.
Xét \(\Delta BNC\) và \(\Delta CMB\) có:
\(\begin{array}{l}BN = AN = \dfrac{{AB}}{2};\,\\CM = AM = \dfrac{{AC}}{2}\end{array}\)
Mà \(AB = AC\) \( \Rightarrow BN = CM\)
Lại có:
+) \(\widehat B = \widehat C\) (do \(\Delta ABC\) cân tại A)
+) \(BC\) cạnh chung.
Do đó: \(\Delta BNC = \Delta CMB \left( {c.g.c} \right)\).
Tam giác\(\,\Delta BKC\) là tam giác.
-
A
Cân tại \(K\)
-
B
Cân tại \(B\)
-
C
Cân tại \(C\)
-
D
Đều
Đáp án của giáo viên lời giải hay : A
Sử dụng kết quả câu trước: \(\Delta BNC = \Delta CMB\)
Chứng minh hai góc ở đáy của tam giác bằng nhau.
Theo câu trước ta có: \(\Delta BNC = \Delta CMB\)
Do \(\Delta BNC = \Delta CMB\)
\( \Rightarrow \widehat {MBC} = \widehat {NCB}\) (hai góc tương ứng)
\( \Rightarrow \Delta KBC\) cân tại \(K.\)
Chọn câu đúng.
-
A
\(BC = 4KM\)
-
B
\(BC > 4KM\)
-
C
\(BC < 4KM\)
-
D
\(BC = 5KM\)
Đáp án của giáo viên lời giải hay : C
Sử dụng kết quả câu trước: \(\Delta KBC\) cân tại \(K.\)
Áp dụng tính chất tam giác cân, đường trung tuyến và bất đẳng thức tam giác để có kết quả đúng.
Ta có: \(\Delta KBC\) cân tại \(K\) (theo câu trước)
\( \Rightarrow BK = CK\)
Ta có: \(BK + CK = BK + BK = 2BK = 2.2KM = 4KM\) (tính chất đường trung tuyến).
Mà \(\Delta KBC\) có: \(KB + KC > BC\) (bất đẳng thức tam giác)
Suy ra: \(BC < 4.KM\)
Biết \(\dfrac{{bz - cy}}{a} = \dfrac{{cx - az}}{b} = \dfrac{{ay - bx}}{c}\) (với a, b, c \( \ne \)0).
-
A
\(\dfrac{a}{x} = \dfrac{b}{y} = \dfrac{c}{z}\)
-
B
\(\dfrac{a}{y} = \dfrac{b}{x} = \dfrac{c}{z}\)
-
C
\(\dfrac{a}{z} = \dfrac{b}{y} = \dfrac{c}{x}\)
-
D
\(\dfrac{a}{x} = \dfrac{b}{z} = \dfrac{c}{y}\)
Đáp án của giáo viên lời giải hay : A
Sử dụng tính chất tỉ lệ thức \(\dfrac{a}{b} = \dfrac{c}{d} = \dfrac{{ka}}{{kb}} = \dfrac{{mc}}{{md}} = \dfrac{{ka + mc}}{{kb + md}}\).
Ta có:
\(\begin{array}{l}\dfrac{{bz - cy}}{a} = \dfrac{{cx - az}}{b} = \dfrac{{ay - bx}}{c}\\ = \dfrac{{abz - acy}}{{{a^2}}} = \dfrac{{bcx - abz}}{{{b^2}}} \\= \dfrac{{acy - bcx}}{{{c^2}}}\\ = \dfrac{{abz - acy + bcx - abz + acy - bcx}}{{{a^2} + {b^2} + {c^2}}} \\= \dfrac{0}{{{a^2} + {b^2} + {c^2}}} = 0\end{array}\).
Suy ra: \(\dfrac{{bz - cy}}{a} = 0\), do đó \(bz = cy\) hay \(\dfrac{y}{b} = \dfrac{z}{c}(1)\)
\(\dfrac{{cx - az}}{b} = 0\), do đó \(cx = az\) hay \(\dfrac{z}{c} = \dfrac{x}{a}(2)\)
Từ (1) và (2) suy ra: \(\dfrac{a}{x} = \dfrac{b}{y} = \dfrac{c}{z}.\)
