Biểu thức nào sau đây được gọi là đơn thức.
-
A
\(\left( {2 + x} \right).{x^2}\)
-
B
\(2 + {x^2}\)
-
C
\(67{x^2}\)
-
D
\(2y + 1\)
Đáp án của giáo viên lời giải hay : C
Đơn thức là biểu thức đại số chỉ gồm một số hoặc một biến, hoặc một tích giữa các số và biến.
Đơn thức là biểu thức đại số chỉ gồm một số hoặc một biến, hoặc một tích giữa các số và biến.
Đơn thức nào sau đây đồng dạng với đơn thức \( - \dfrac{2}{3}x{y^2}\).
-
A
\(3xy\left( { - 2y} \right)\)
-
B
\(\dfrac{{ - 2}}{3}{\left( {xy} \right)^2}\)
-
C
\( - \dfrac{3}{2}{x^2}y\)
-
D
\(\dfrac{{ - 2}}{3}xy\)
Đáp án của giáo viên lời giải hay : A
Hai đơn thức đồng dạng là hai đơn thức có hệ số khác không và có cùng phần biến.
Ta có: \(3xy\left( { - 2y} \right) = - 6x{y^2}\) có cùng phần biến với \( - \dfrac{2}{3}x{y^2}\).
Vậy hai đơn thức đó đồng dạng với nhau.
Bậc của đa thức \(M = {x^6} + 5{x^2}{y^2} + {y^4} - {x^4}{y^3} - 25\) là:
-
A
\(4\)
-
B
\(5\)
-
C
\(6\)
-
D
\(7\)
Đáp án của giáo viên lời giải hay : D
Thu gọn đa thức nếu có thể.
Bậc của đa thức là bậc của hạng tử có bậc cao nhất trong dạng thu gọn của đa thức đó.
Ta có: \(M = {x^6} + 5{x^2}{y^2} + {y^4} - {x^4}{y^3} - 25\)
Đa thức này đã là đa thức thu gọn.
Trong đa thức: \(M = {x^6} + 5{x^2}{y^2} + {y^4} - {x^4}{y^3} - 25\).
Hạng tử: \({x^6}\) có bậc 6. Hạng tử: \({x^2}{y^2}\) có bậc 4. Hạng tử \({y^4}\) có bậc 4. Hạng tử \( - {x^4}{y^3}\) có bậc 7. Hạng tử \( - 25\) có bậc 0.
Bậc cao nhất trong các bậc đó là 7.
\( \Rightarrow M\) có bậc là 7.
Trong tam giác \(M{\rm N}P\) có điểm \(O\) cách đều 3 đỉnh tam giác. Khi đó O là giao điểm của:
-
A
ba đường cao
-
B
ba đường trung trực
-
C
ba đường trung tuyến
-
D
ba đường phân giác
Đáp án của giáo viên lời giải hay : B
Định lý tính chất ba đường trung trực của tam giác: Ba đường trung trực của một tam giác cùng đi qua một điểm. Điểm này cách đều ba đỉnh của tam giác đó.
Vì O cách đều 3 đỉnh của tam giác nên O là giao điểm của ba đường trung trực.
Cách sắp xếp nào của đa thức sau đây theo lũy thừa giảm dần của biến x là đúng?
-
A
\(1 + 4{x^5} - 3{x^4} + 5{x^3} - {x^2} + 2x\)
-
B
\(5{x^3} + 4{x^5} - 3{x^4} + 2x - {x^2} + 1\)
-
C
\(4{x^5} - 3{x^4} + 5{x^3} - {x^2} + 2x + 1\)
-
D
\(1 + 2x - {x^2} + 5{x^3} - 3{x^4} + 4{x^5}\)
Đáp án của giáo viên lời giải hay : C
Quan sát các đa thức: chú ý tới lũy thừa của các biến, đa thức nào có lũy thừa giảm dần.
Ta thấy cách sắp xếp theo lũy thừa giảm dần của biến x là: \(4{x^5} - 3{x^4} + 5{x^3} - {x^2} + 2x + 1\).
Giá trị của biểu thức \(5{x^2}y + 10{y^2}x\) tại \(x = - 2\) và \(y = - 1\) là:
-
A
\(10\)
-
B
\( - 10\)
-
C
\(40\)
-
D
\( - 40\)
Đáp án của giáo viên lời giải hay : D
Thay các giá trị \(x = - 2\) và \(y = - 1\) vào biểu thức \(5{x^2}y + 10{y^2}x\).
Thay các giá trị \(x = - 2\) và \(y = - 1\) vào biểu thức \(5{x^2}y + 10{y^2}x\) ta được:
\(\begin{array}{l}5{x^2}y + 10{y^2}x = 5. {\left( { - 2} \right)^2}. \left( { - 1} \right) + 10. {\left( { - 1} \right)^2}. \left( { - 2} \right)\\ = 5. 4. \left( { - 1} \right) + 10. 1. \left( { - 2} \right)\\ = - 20 - 20 = - 40\end{array}\).
Số nào sau đây là nghiệm của đa thức \(g\left( y \right) = \dfrac{2}{3}y + 2\).
-
A
\(6\)
-
B
\(3\)
-
C
\(- 3\)
-
D
\(- 6\)
Đáp án của giáo viên lời giải hay : C
Nghiệm của đa thức một biến: Nếu tại \(x = a\), đa thức \(P\left( x \right)\) có giá trị bằng 0 thì ta nói a (hoặc \(x = a\)) là một nghiệm của đa thức đó.
Ta có: \(g\left( y \right) = 0 \Leftrightarrow \dfrac{2}{3}y + 2 = 0\) \( \Leftrightarrow \dfrac{2}{3}y = - 2 \Leftrightarrow y = - 3\).
Vậy \(y = - 3\) là nghiệm của đa thức \(g\left( y \right) = \dfrac{2}{3}y + 2\).
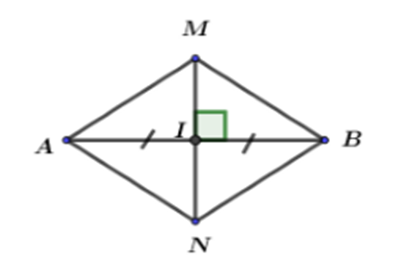
Cho hình vẽ, ta có MN là đường trung trực của đoạn thẳng AB và \(MI > {\rm N}I\). Khi đó ta có:
-
A
\(MA = {\rm N}B\)
-
B
\(MA > {\rm N}B\)
-
C
\(MA < {\rm N}B\)
-
D
\(MA//{\rm N}B\)
Đáp án của giáo viên lời giải hay : B
Dựa vào mối quan hệ giữa đường xiên và hình chiếu.
AM có hình chiếu MI, NB có hình chiếu NI.
Lưu ý: Đường xiên có hình chiếu lớn hơn thì lớn hơn.
Ta có: MN là đường trung trực của đoạn thẳng AB và \(MI > {\rm N}I\)
Lại có AM có hình chiếu MI, NB có hình chiếu NI.
Mà: \(MI > {\rm N}I \Rightarrow AM > {\rm N}B\) (đường xiên có hình chiếu lớn hơn thì lớn hơn).
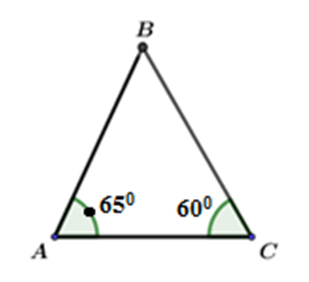
Tam giác \(ABC\) có các số đo như hình dưới, ta có:
-
A
\(BC > AB > AC\)
-
B
\(AB > BC > AC\)
-
C
\(AC > AB > BC\)
-
D
\(BC > AC > AB\)
Đáp án của giáo viên lời giải hay : A
Dựa vào định lý tổng ba góc của một tam giác, ta tính được góc còn lại (góc B).
Sử dụng mối quan hệ giữa góc và cạnh đối diện trong một tam giác: Trong một tam giác cạnh đối diện với góc lớn hơn là cạnh lớn hơn.
Xét tam giác \(ABC\), ta có:
\(\begin{array}{l}\widehat A + \widehat B + \widehat C = {180^0}\\ \Rightarrow \widehat B = {180^0} - \left( {\widehat A + \widehat C} \right)\\ = {180^0} - \left( {{{65}^0} + {{60}^0}} \right)\\ = {180^0} - {125^0}\\ = \,{55^0}\end{array}\)
\( \Rightarrow \widehat A > \widehat C > \widehat B \Rightarrow BC > AB > AC\) (trong một tam giác cạnh đối diện với góc lớn hơn là cạnh lớn hơn).
Bộ ba số đo nào sau đây có thể là độ dài ba cạnh của một tam giác vuông?
-
A
\(3cm,\,9cm,\,14cm\)
-
B
\(2cm,\,3cm,\,5cm\)
-
C
\(4cm,\,9cm,\,12cm\)
-
D
\(6cm,\,8cm,\,10cm\)
Đáp án của giáo viên lời giải hay : D
Ta kiểm tra từng bộ ba số, bộ số nào thỏa mãn định lý Pytago đảo thì kết luận, bộ ba đó chính là độ dài ba cạnh của một tam giác vuông.
Định lý Pytago đảo: Trong một tam giác nếu bình phương một cạnh bằng tổng bình phương hai cạnh còn lại thì tam giác đó là tam giác vuông.
Trong tam giác vuông, cạnh huyền lớn nhất.
Ta có:
\(\begin{array}{l} + )\,\,{14^2} = 196 \ne {9^2} + {7^2}\\ + )\,\,{5^2} = 25\,\, \ne \,\,{2^2} + {3^2} = 13\\ + )\,\,{12^2} = 144 \ne {4^2} + {9^2} = 97\\ + )\,{10^2} = 100 = {6^2} + {8^2}\end{array}\).
Chỉ có bộ \(6cm,\,8cm,\,10cm\) thỏa mãn định lý Pi-ta-go đảo. Vậy bộ ba số này là độ dài 3 cạnh của một tam giác vuông.
Tam giác cân có góc ở đỉnh là \({80^o}\). Số đo góc ở đáy là:
-
A
\({50^o}\)
-
B
\({80^o}\)
-
C
\({100^o}\)
-
D
\({120^o}\)
Đáp án của giáo viên lời giải hay : A
+) Áp dụng định lí tổng ba góc của tam giác để tìm tổng số đo hai góc ở đáy.
+) Áp dụng tính chất của tam giác cân “số đo hai góc kề cạnh đáy bằng nhau” để tìm số đo góc ở đáy.
Giả sử tam giác ABC cân tại A có: \(\widehat A = {80^o}\). Ta sẽ tìm số đo góc B hoặc góc C.
Áp dụng định lí tổng ba góc trong tam giác ta có: \(\widehat A + \widehat B + \widehat C = {180^o}\)
\( \Rightarrow \widehat B + \widehat C = {180^o} - \widehat A = {180^o} - {80^o} = {100^o}\)
Do tam giác ABC cân tại A nên \(\widehat B = \widehat C\). Từ đó suy ra: \(\widehat B = \widehat C = \dfrac{{\widehat B + \widehat C}}{2} = \dfrac{{{{100}^o}}}{2} = {50^o}\).
Vậy số đo góc ở đáy là \({50^o}\).
Cho hai đa thức: \(P\left( x \right) = 2{x^2} - 10\) và \(Q\left( x \right) = {x^2} + x + 5\). Hiệu \(P\left( x \right) - Q\left( x \right)\) bằng:
-
A
\({x^2} - 15\)
-
B
\({x^2} - x - 15\)
-
C
\(2{x^2} - 5\)
-
D
\(3{x^2} - x - 2\)
Đáp án của giáo viên lời giải hay : B
Thực hiện phép trừ hai đa thức. Để trừ hai đa thức, ta thực hiện như sau:
Bước 1: Viết các hạng tử của đa thức thứ nhất cùng với dấu của chúng.
Bước 2: Viết tiếp các hạng tử của đa thức thứ hai với dấu ngược lại.
Bước 3: Thu gọn các hạng tử đồng dạng.
Chú ý: Nếu là phép cộng ta thực hiện bước 1 và bước 3, bỏ qua bước 2.
Nếu là phép trừ, ta thực hiện đầy đủ cả ba bước.
Ta có:
\(\begin{array}{l}P\left( x \right) - Q\left( x \right) = 2{x^2} - 10 - \left( {{x^2} + x + 5} \right)\\ = 2{x^2} - 10 - {x^2} - x - 5\\ = {x^2} - x - 15\end{array}\).
Cho \(\Delta MNP\) có \(\widehat M = {40^0}\), các đường phân giác \(NH\) và \(PK\) của \(\widehat N\) và \(\widehat P\) cắt nhau tại I. Khi đó \(\widehat {NIP}\) bằng:
-
A
\({70^o}\)
-
B
\({80^o}\)
-
C
\({110^o}\)
-
D
\({140^o}\)
Đáp án của giáo viên lời giải hay : C
+) Áp dụng định lí tổng ba góc của tam giác.
+) Áp dụng tính chất tia phân giác của một góc trong tam giác.
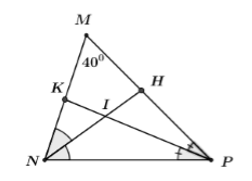
Xét \(\Delta MNP\) có: \(\widehat M + \widehat {MNP} + \widehat {MPN} = {180^0}\) (định lý tổng ba góc trong một tam giác)
\( \Rightarrow \widehat {MNP} + \widehat {MPN} = {180^0} - \widehat M = {180^0} - {40^0} = {140^0}\left( 1 \right)\)
Vì NH là phân giác của \(\widehat {MNP}\left( {gt} \right) \Rightarrow \widehat {HNP} = \dfrac{{\widehat {MNP}}}{2}\left( 2 \right)\) (tính chất tia phân giác)
Vì PK là phân giác của \(\widehat {MNP}\left( {gt} \right) \Rightarrow \widehat {NPK} = \dfrac{{\widehat {MPN}}}{2}\left( 3 \right)\) (tính chất tia phân giác)
Từ (1) (2) và (3) \( \Rightarrow \widehat {INP} + \widehat {IPN} = \dfrac{{\widehat {MNP}}}{2} + \dfrac{{\widehat {MPN}}}{2} = {140^0}:2 = {70^0}\) hay \(\widehat {INP} + \widehat {IPN} = {70^0}\left( * \right)\)
Xét \(\Delta INP\) có: \(\widehat {INP} + \widehat {IPN} + \widehat {NIP} = {180^0}\left( {**} \right)\)( định lý tổng ba góc trong một tam giác)
Từ (*) và (**) \( \Rightarrow \widehat {NIP} = {180^0} - \left( {\widehat {INP} + \widehat {IPN}} \right) = {180^0} - {70^0} = {110^0}\)
Tính giá trị biểu thức sau bằng cách hợp lý:
\(A = \dfrac{3}{4}.\dfrac{5}{{14}} + \dfrac{6}{7}:\dfrac{4}{3} - 1\dfrac{1}{7}:1\dfrac{1}{3}\).
-
A
\(A = - \dfrac{3}{{14}}\)
-
B
\(A = \dfrac{3}{{14}}\)
-
C
\(A = - \dfrac{3}{{56}}\)
-
D
\(A = \dfrac{3}{{56}}\)
Đáp án của giáo viên lời giải hay : D
Đưa hỗn số về dạng phân số.
Sử dụng \(AB + AC = A\left( {B + C} \right)\).
Ta có: \(A = \dfrac{3}{4}.\dfrac{5}{{14}} + \dfrac{6}{7}:\dfrac{4}{3} - 1\dfrac{1}{7}:1\dfrac{1}{3}\)
\(\begin{array}{l} = \dfrac{3}{4}.\dfrac{5}{{14}} + \dfrac{6}{7}.\dfrac{3}{4} - \dfrac{8}{7}:\dfrac{4}{3}\\ = \dfrac{3}{4}.\dfrac{5}{{14}} + \dfrac{6}{7}.\dfrac{3}{4} - \dfrac{8}{7}.\dfrac{3}{4}\\ = \dfrac{3}{4}\left( {\dfrac{5}{{14}} + \dfrac{6}{7} - \dfrac{8}{7}} \right)\\ = \dfrac{3}{4}\left( {\dfrac{5}{{14}} - \dfrac{2}{7}} \right)\\ = \dfrac{3}{4}.\dfrac{1}{{14}}\\ = \dfrac{3}{{56}}\end{array}\).
Vậy \(A = \dfrac{3}{{56}}.\)
Tìm \(x\) biết \(\left( { - 1\dfrac{3}{5} + x} \right).\dfrac{{14}}{{15}} = 2\dfrac{1}{3}\).
-
A
\(x = - \dfrac{{41}}{{10}}\)
-
B
\(x = \dfrac{{41}}{{10}}\)
-
C
\(x = \dfrac{{31}}{{10}}\)
-
D
\(x = \dfrac{{41}}{7}\)
Đáp án của giáo viên lời giải hay : B
Sử dụng cách tìm \(x\) đã học để tính toán:
+ Muốn tìm thừa số chưa biết ta lấy tích chia cho thừa số đã biết.
+ Muốn tìm số hạng chưa biết ta lấy tổng trừ cho số hạng đã biết.
Ta có: \(\left( { - 1\dfrac{3}{5} + x} \right).\dfrac{{14}}{{15}} = 2\dfrac{1}{3}\)
\(\begin{array}{l} \Leftrightarrow \left( { - \dfrac{8}{5} + x} \right).\dfrac{{14}}{{15}} = \dfrac{7}{3}\\ \Leftrightarrow - \dfrac{8}{5} + x = \dfrac{7}{3}:\dfrac{{14}}{{15}}\\ \Leftrightarrow - \dfrac{8}{5} + x = \dfrac{7}{3}.\dfrac{{15}}{{14}}\\ \Leftrightarrow - \dfrac{8}{5} + x = \dfrac{5}{2}\\ \Leftrightarrow x = \dfrac{5}{2} + \dfrac{8}{5}\\ \Leftrightarrow x = \dfrac{{25 + 16}}{{10}}\\ \Leftrightarrow x = \dfrac{{41}}{{10}}\end{array}\).
Cho các đa thức:
\(\begin{array}{l}f\left( x \right) = {x^3} - 2{x^2} + 3x + 1\\g\left( x \right) = {x^3} + x - 1\\h\left( x \right) = 2{x^2} - 1\end{array}\).
Tính: \(f\left( x \right) - g\left( x \right) + h\left( x \right)\).
-
A
\(f\left( x \right) - g\left( x \right) + h\left( x \right) = 2x\)
-
B
\(f\left( x \right) - g\left( x \right) + h\left( x \right) = 2x + 1\)
-
C
\(f\left( x \right) - g\left( x \right) + h\left( x \right) = 2x + 3\)
-
D
\(f\left( x \right) - g\left( x \right) + h\left( x \right) = 4{x^2} + 2x + 1\)
Đáp án của giáo viên lời giải hay : B
Thực hiện cộng các đa thức. Để cộng, trừ hai đa thức, ta thực hiện như sau:
Bước 1: Viết các hạng tử của đa thức thứ nhất cùng với dấu của chúng.
Bước 2: Viết tiếp các hạng tử của đa thức thứ hai.
Bước 3: Thu gọn các hạng tử đồng dạng.
\(\begin{array}{l}\,f\left( x \right) = {x^3} - 2{x^2} + 3x + 1\\g\left( x \right) = {x^3} + x - 1\\h\left( x \right) = 2{x^2} - 1\\ \Rightarrow f\left( x \right) - g\left( x \right) + h\left( x \right)\\ = {x^3} - 2{x^2} + 3x + 1 - \left( {{x^3} + x - 1} \right) + \left( {2{x^2} - 1} \right)\\ = \,{x^3} - 2{x^2} + 3x + 1 - {x^3} - x + 1 + 2{x^2} - 1\\ = \left( {{x^3} - {x^3}} \right) + \left( { - 2{x^2} + 2{x^2}} \right) + \left( {3x - x} \right) + 1 + 1 - 1\\ = 2x + 1\end{array}\).
Vậy \(f\left( x \right) - g\left( x \right) + h\left( x \right) = 2x + 1.\)
Tìm x sao cho \(f\left( x \right) - g\left( x \right) + h\left( x \right) = 0.\)
-
A
\(x = \dfrac{{ - 1}}{2}\)
-
B
\(x = \dfrac{1}{2}\)
-
C
\(x = - 2\)
-
D
\(x = 2\)
Đáp án của giáo viên lời giải hay : A
Sử dụng kết quả câu trước \(f\left( x \right) - g\left( x \right) + h\left( x \right) = 2x + 1\) rồi cho \(f\left( x \right) - g\left( x \right) + h\left( x \right) = 0\,\) để tìm x.
Ta có:
\(\begin{array}{l}f\left( x \right) - g\left( x \right) + h\left( x \right) = 0\\ \Leftrightarrow 2x + 1 = 0\\ \Leftrightarrow 2x\,\,\,\,\,\,\,\, = - 1\\ \Leftrightarrow \,\,\,\,x\,\,\,\,\,\,\,\, = \dfrac{{ - 1}}{2}\end{array}\).
Vậy \(x = \dfrac{{ - 1}}{2}.\)
Cho góc nhọn \(xOy.\) Điểm H nằm trên tia phân giác của góc \(xOy.\) Hạ \(HA \,\bot \,{\rm{Ox,}}\,{\rm{HB}} \,\bot \,{\rm{Oy}}\) \(\left( {A \in {\rm{Ox}},\,B \in Oy} \right)\). Gọi D là hình chiếu của điểm A trên Oy, C là giao điểm của AD với OH.
Tam giác \(HAB\) là tam giác:
-
A
đều
-
B
cân tại \(H\)
-
C
cân tại \(B\)
-
D
cân tại \(A\)
Đáp án của giáo viên lời giải hay : B
Tính chất các điểm nằm trên tia phân giác: Điểm nằm trên tia phân giác của một góc thì cách đều hai cạnh của góc đó. Từ đó chỉ ra hai cạnh \(HB = HA\).
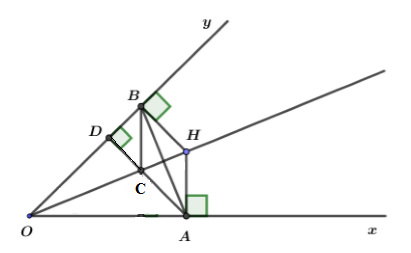
Vì \(H\) nằm trên tia phân giác của góc \(xOy\)
mà \(HA \,\bot \,{\rm{Ox,}}\,{\rm{HB}} \,\bot \,{\rm{Oy}}\) nên ta có:
\(HA = HB\) (tính chất các điểm thuộc tia phân giác)
\( \Rightarrow \Delta HAB\) cân tại \(H\).
Chọn câu đúng.
-
A
\(OA = OB\)
-
B
\(OC\) là phân giác góc \(xOy\)
-
C
\(BC \,\bot \,{\rm{Ox}}\)
-
D
Cả A, B, C đều đúng
Đáp án của giáo viên lời giải hay : D
+) Chứng minh hai tam giác bằng nhau rồi suy ra cặp cạnh bằng nhau
+) Chứng minh C là trực tâm của tam giác \(OAB\).
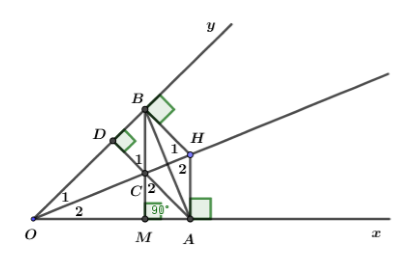
Xét hai tam giác vuông \(HBO\) và \(HAO\) ta có:
Cạnh huyền \(OH\,chung\)
Góc nhọn \({O_1} = {O_2}\)
\( \Rightarrow \Delta HBO = \Delta HAO\,\) (cạnh huyền-góc nhọn)
Do đó: \(OA = OB\) (cạnh tương ứng)
Xét tam giác \(OAB\) cân tại O do \(OA = OB\) (cmt)
Mà \(AD \bot BO\) \( \Rightarrow AD\) là đường cao.
C nằm trên tia phân giác góc O. Hay OC là đường phân giác góc O.
Trong một tam giác cân đường phân giác cũng chính là đường cao.
Mặt khác CO giao với AD tại C.
\( \Rightarrow C\) là trực tâm của tam giác OAB.
Do đó BC là đường cao.
Hay \(BC \bot OA\) hay \(BC \bot {\rm{Ox}}\)
Khi \(\widehat {xOy} = {60^0}\) thì ta có:
-
A
\(OA = 2OD\)
-
B
\(OA = 3OD\)
-
C
\(3OA = 2OD\)
-
D
\(2OA = 3OD\)
Đáp án của giáo viên lời giải hay : A
Chứng minh khi \(\widehat {xOy} = {60^0}\) thì tam giác \({\rm N}OD\) là tam giác đều, từ đó suy ra \(OD = O{\rm N}\).
Sau đó lập luận để có mối quan hệ đúng.
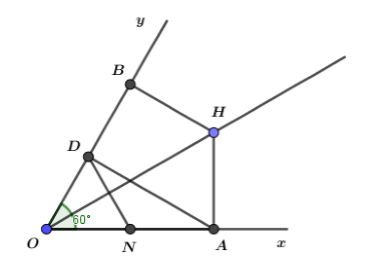
Gọi N là trung điểm của OA, khi đó trong tam giác vuông AOD (vuông tại D)
Khi đó \(D{\rm N} = O{\rm N} = \dfrac{{OA}}{2}\) (đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền)
\( \Rightarrow \Delta {\rm N}OD\) cân tại N (1)
Mặt khác \(\widehat {AOD} = \widehat {xOy} = {60^0}\) (2)
Từ (1) và (2), suy ra \(\Delta {\rm N}OD\) là tam giác đều.
\( \Rightarrow OD = O{\rm N}\) mà \(O{\rm N} = \dfrac{1}{2}OA\)
\( \Rightarrow OD = \dfrac{1}{2}OA\,\,hay\,\,OA = 2OD\).
Số cây của ba tổ trồng tỉ lệ với số học sinh của mỗi tổ, tổng số cây ba tổ trồng được là \(135\) cây. Tìm số cây của tổ 3 đã trồng, biết tổ 1 có 7 bạn, tổ 2 có 8 bạn và tổ 3 có 12 bạn.
-
A
\(60\) cây
-
B
\(40\) cây
-
C
\(35\) cây
-
D
\(48\) cây
Đáp án của giáo viên lời giải hay : A
Sử dụng tính chất tỉ lệ thức: \(\dfrac{a}{b} = \dfrac{c}{d} = \dfrac{e}{f} = \dfrac{{a + c + e}}{{b + d + f}}\).
Gọi số cây tổ 1, tổ 2, tổ 3 trồng được lần lượt là: \(x,y,z\,\,\left( {x;y;z \in {\mathbb{N}^*}} \right)\) (cây).
Ba tổ trồng được \(135\) cây nên ta có \(x + y + z = 135\).
Vì số cây của ba tổ trồng tỉ lệ với số học sinh của mỗi tổ nên \(\dfrac{x}{7} = \dfrac{y}{8} = \dfrac{z}{{12}}\).
Áp dụng tính chất dãy tỉ số bằng nhau ta có \(\dfrac{x}{7} = \dfrac{y}{8} = \dfrac{z}{{12}} = \dfrac{{x + y + z}}{{7 + 8 + 12}} = \dfrac{{135}}{{27}} = 5\) (vì \(x + y + z = 135\)).
Suy ra:
+) \(\dfrac{x}{7} = 5 \Leftrightarrow x = 5.7 = 35\)
+) \(\dfrac{y}{8} = 5 \Leftrightarrow y = 5.8 = 40\)
+) \(\dfrac{z}{{12}} = 5 \Leftrightarrow z = 5.12 = 60\)
Vậy số cây tổ 3 trồng được là \(60\) cây.
Tìm giá trị nhỏ nhất của biểu thức \({\left( {{x^2} - 9} \right)^2} + \left| {y - 3} \right| - 1\).
-
A
\( - 1\)
-
B
\(1\)
-
C
\(3\)
-
D
\(9\)
Đáp án của giáo viên lời giải hay : A
Nhận thấy \({\left( {{x^2} - 9} \right)^2} \ge 0\) và \(\left| {y - 3} \right| \ge 0\) từ đó biến đổi sao cho về biểu thức \({\left( {{x^2} - 9} \right)^2} + \left| {y - 3} \right| - 1\), rồi biến đổi sao cho biểu thức có dạng \(M \ge a\). Khi đó a chính là GTNN của biểu thức đã cho. Chú ý: Tìm x, y để dấu bằng xảy ra.
Đặt \(A = {\left( {{x^2} - 9} \right)^2} + \left| {y - 3} \right| - 1\).
Ta có:
\(\begin{array}{l}{\left( {{x^2} - 9} \right)^2} \ge 0;\,\left| {y - 3} \right|\,\, \ge 0\\ \Rightarrow {\left( {{x^2} - 9} \right)^2} + \left| {y - 3} \right| - 1 \ge 0 + 0 - 1\\ \Rightarrow {\left( {{x^2} - 9} \right)^2} + \left| {y - 3} \right| - 1 \ge - 1\end{array}\).
Hay \(A \ge - 1\). Dấu xảy ra khi và chỉ khi: \(\left\{ \begin{array}{l}{x^2} - 9 = 0\\y - 3 = 0\end{array} \right.\) hay \(x = - 3\) hoặc \(x = 3\) và \(y = 3\)
Vậy giá trị nhỏ nhất của A là: \(A = - 1\) khi \(x = - 3;y = 3\) hoặc \(x = y = 3\).
