
Tỉ số của số thứ nhất và số thứ hai là \(\dfrac{9}{7}\) thì khi vẽ sơ đồ ta vẽ:
A. Số thứ nhất là \(7\) phần, số thứ hai là \(9\) phần
B. Số thứ nhất là \(9\) phần, số thứ hai là \(7\) phần
C. Số thứ nhất là \(7\) phần, số thứ hai là \(16\) phần
D. Số thứ nhất là \(9\) phần, số thứ hai là \(16\) phần
B. Số thứ nhất là \(9\) phần, số thứ hai là \(7\) phần
Dựa vào tỉ số của hai số.
Tỉ số của số thứ nhất và số thứ hai là \(\dfrac{9}{7}\) có nghĩa số thứ nhất bằng \(\dfrac{9}{7}\) số thứ hai. Vậy nếu coi số thứ hai là \(7\) phần thì số thứ nhất là \(9\) phần như thế.
Vậy đáp án đúng là số thứ nhất là \(9\) phần, số thứ hai là \(7\) phần.

Điền số thích hợp vào ô trống:
Hiệu của hai số là \(57\). Tỉ số của hai số đó là \(\dfrac{2}{5}\).
Vậy số bé là
Hiệu của hai số là \(57\). Tỉ số của hai số đó là \(\dfrac{2}{5}\).
Vậy số bé là
Bài toán cho biết hiệu và tỉ số của hai số. Đây là dạng toán tìm hai số khi biết hiệu và tỉ số của 2 số đó.
Theo bài ra tỉ số của hai số đó là \(\dfrac{2}{5}\) nên ta vẽ sơ đồ biểu thị số bé gồm \(2\) phần, số lớn gồm \(5\) phần như thế. Ta tìm số bé theo công thức:
Số bé = (Hiệu : hiệu số phần bằng nhau) × số phần của số bé
Ta có sơ đồ:
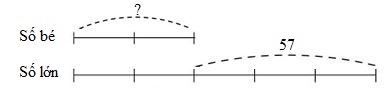
Theo sơ đồ, hiệu số phần bằng nhau là:
\(5 - 2 = 3\) (phần)
Số bé là:
\(57:3 \times 2 = 38\)
Đáp số: \(38\).
Vậy đáp án đúng điền vào ô trống là \(38\).

Hiệu của hai số là \(156\). Tỉ số của hai số đó là \(\dfrac{5}{7}\). Vậy hai số đó là:
A. \(395\,\,;\,\,541\)
B. \(390\,\,;\,\,546\)
C. \(385\,\,;\,\,551\)
D. \(380\,\,;\,\,556\)
B. \(390\,\,;\,\,546\)
Bài toán cho biết hiệu và tỉ số của hai số. Đây là dạng toán tìm hai số khi biết hiệu và tỉ số của 2 số đó.
Theo bài ra tỉ số của hai số đó là \(\dfrac{5}{7}\) nên ta vẽ sơ đồ biểu thị số bé gồm \(5\) phần, số lớn gồm \(7\) phần như thế. Ta tìm hai số theo công thức:
Số bé = (hiệu : hiệu số phần bằng nhau) × số phần của số bé
hoặc
Số lớn = (hiệu : hiệu số phần bằng nhau) × số phần của số lớn.
Ta có sơ đồ:
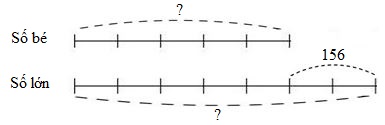
Theo sơ đồ, hiệu số phần bằng nhau là:
\(7 - 5 = 2\) (phần)
Số bé là:
\(156:2 \times 5 = 390\)
Số lớn là:
\(390 + 156 = 546\)
Đáp số: Số bé: \(390\) ;
Số lớn: \(546\).

Một cửa hàng có số gạo tẻ nhiều hơn số gạo nếp là \(135kg\). Biết số gạo nếp bằng \(\dfrac{3}{8}\) số gạo tẻ. Tính số gạo mỗi loại?
A. \(212kg\) gạo tẻ; \(77kg\) gạo nếp
B. \(222kg\) gạo tẻ; \(87kg\) gạo nếp
C. \(216kg\) gạo tẻ; \(81kg\) gạo nếp
D. \(225kg\) gạo tẻ; \(90kg\) gạo nếp
C. \(216kg\) gạo tẻ; \(81kg\) gạo nếp
Bài toán cho biết hiệu và tỉ số của gạo tẻ và gạo nếp.
Đây là dạng toán tìm hai số khi biết hiệu và tỉ số của 2 số đó.
Theo bài ra số gạo nếp bằng \(\dfrac{3}{8}\) số gạo tẻ nên ta vẽ sơ đồ biểu thị số gạo nếp gồm \(3\) phần, số gạo tẻ gồm \(8\) phần như thế. Cọi số gạo nếp là số bé, số gạo tẻ là số lớn, ta tìm hai số theo công thức:
Số bé = (hiệu : hiệu số phần bằng nhau) × số phần của số bé
hoặc
Số lớn = (hiệu : hiệu số phần bằng nhau) × số phần của số lớn.
Ta có sơ đồ:
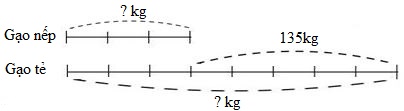
Theo sơ đồ, hiệu số phần bằng nhau là:
\(8 - 3 = 5\) (phần)
Cửa hàng đó có số ki-lô-gam gạo tẻ là:
\(135:5 \times 8 = 216\,\,(kg)\)
Cửa hàng đó có số ki-lô-gam gạo nếp là:
\(216 - 135 = 81\,\,(kg)\)
Đáp số: \(216kg\) gạo tẻ;
\(81kg\) gạo nếp.
 Điền số thích hợp vào ô trống:
Điền số thích hợp vào ô trống:
Hiệu của hai số là số chẵn lớn nhất có ba chữ số. Biết số lớn gấp \(3\) lần số bé.
Vậy số lớn là
Hiệu của hai số là số chẵn lớn nhất có ba chữ số. Biết số lớn gấp \(3\) lần số bé.
Vậy số lớn là
- Tìm số chẵn lớn nhất có ba chữ số là \(998\). Vậy hiệu của hai số là \(998\). Khi đó ta có bài toán tìm hai số khi biết hiệu và tỉ số.
- Theo đề bài số lớn gấp \(3\) lần số bé nên ta vẽ sơ đồ biểu thị số bé gồm \(1\) phần, số lớn gồm \(3\) phần như thế. Ta tìm số lớn theo công thức:
Số lớn = (Hiệu : hiệu số phần bằng nhau) × số phần của số lớn.
Số chẵn lớn nhất có ba chữ số là \(998\). Vậy hiệu của hai số là \(998\).
Ta có sơ đồ:
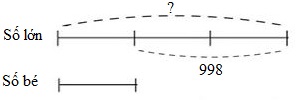
Theo sơ đồ, hiệu số phần bằng nhau là:
\(3 - 1 = 2\) (phần)
Số lớn là:
\(998:2 \times 3 = 1497\)
Đáp số: \(1497\).
Vậy đáp án đúng điền vào ô trống là \(1497\).

Giải bài toán theo sơ đồ sau:
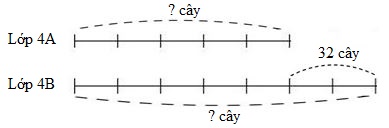
A. Lớp 4A: $90$ cây ; lớp 4B: \(122\) cây.
B. Lớp 4A: $75$ cây ; lớp 4B: \(107\) cây.
C. Lớp 4A: $85$ cây ; lớp 4B: \(117\) cây.
D. Lớp 4A: $80$ cây ; lớp 4B: \(112\) cây.
D. Lớp 4A: $80$ cây ; lớp 4B: \(112\) cây.
Quan sát sơ đồ ta trong đó hiệu số cây trồng được của hai lớp là \(32\) cây, số cây lớp 4A trồng được bằng \(\dfrac{5}{7}\) số cây lớp 4B trồng được. Ta xác định được đây là bài toán tìm hai số khi biết hiệu và tỉ số của hai số đó. Coi số cây lớp 4A trồng được là số bé, số cây lớp 4B trồng được số lớn, ta tìm hai số theo công thức:
Số bé = (hiệu : hiệu số phần bằng nhau) × số phần của số bé
hoặc
Số lớn = (hiệu : hiệu số phần bằng nhau) × số phần của số lớn.
Theo sơ đồ, hiệu số phần bằng nhau là:
\(7 - 5 = 2\) (phần)
Lớp 4A trồng được số cây là:
\(32:2 \times 5 = 80\) (cây)
Lớp 4B trồng được số cây là:
\(80 + 32 = 112\) (cây)
Đáp số: Lớp 4A: $80$ cây;
Lớp 4B: \(112\) cây.
 Điền số thích hợp vào ô trống:
Điền số thích hợp vào ô trống:
Hiệu của hai số là \(224\), nếu giảm số lớn đi \(5\) lần thì ta được số bé.
Vậy tổng của hai số đó là
Hiệu của hai số là \(224\), nếu giảm số lớn đi \(5\) lần thì ta được số bé.
Vậy tổng của hai số đó là
- Theo đề bài giảm số lớn đi \(5\) lần thì ta được số bé nên tỉ số của số bé và số lớn là \(\dfrac{1}{5}\). Ta biểu diễn số bé bằng \(1\) phần, số lớn bằng \(5\) phần như thế. Ta tìm hai số theo công thức:
Số bé = (Hiệu : hiệu số phần bằng nhau) × số phần của số bé
hoặc
Số lớn = (Hiệu : hiệu số phần bằng nhau) × số phần của số lớn.
- Tìm tổng hai số = số lớn + số bé .
Theo đề bài giảm số lớn đi \(5\) lần thì ta được số bé nên tỉ số của số bé và số lớn là \(\dfrac{1}{5}\).
Ta có sơ đồ:
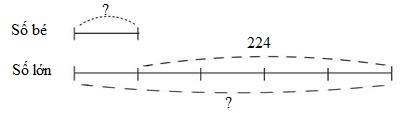
Theo sơ đồ, hiệu số phần bằng nhau là:
\(5 - 1 = 4\) (phần)
Số lớn là:
\(224:4 \times 5 = 280\)
Số bé là:
\(280 - 224 = 56\)
Tổng hai số đó là:
\(280 + 56 = 336\)
Đáp số: \(336\).
Vậy đáp án đúng điền vào ô trống là \(336\).

Một thoi có độ dài đường chéo lớn hơn độ dài đường chéo bé là \(51cm\). Tính diện tích hình thoi đó, biết rằng tỉ số giữa độ dài đường chéo lớn và độ dài đường chéo bé là \(\dfrac{7}{4}\) .
A. \(4046c{m^2}\)
B. \(4064c{m^2}\)
C. \(8092c{m^2}\)
D. \(8128c{m^2}\)
A. \(4046c{m^2}\)
- Theo bài ra tỉ số giữa độ dài đường chéo lớn và độ dài đường chéo bé là \(\dfrac{7}{4}\) nên ta vẽ sơ đồ biểu thị đường chéo bé gồm \(4\) phần, đường chéo lớn gồm \(7\) phần như thế. Cọi đường chéo bé là số bé, đường chéo lớn là số lớn, ta tìm hai số theo công thức:
Số bé = (hiệu : hiệu số phần bằng nhau) × số phần của số bé
hoặc
Số lớn = (hiệu : hiệu số phần bằng nhau) × số phần của số lớn.
- Tính diện tích hình thoi ta lấy tích độ dài hai đường chéo chia cho \(2\).
Ta có sơ đồ:
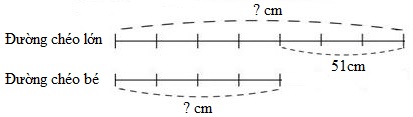
Theo sơ đồ, hiệu số phần bằng nhau là:
\(7 - 4 = 3\) (phần)
Độ dài đường chéo lớn là:
\(51:3 \times 7 = 119\,(cm)\)
Độ dài đường chéo bé là:
\(119 - 51 = 68\,(cm)\)
Diện tích hình thoi đó là:
\(119 \times 68:2 = 4046\,(c{m^2})\)
Đáp số: \(4046c{m^2}\).

Hiện nay mẹ hơn con \(25\) tuổi. Cách đây \(5\) năm tuổi mẹ gấp \(6\) lần tuổi con. Tính tuổi của mỗi người hiện nay.
A. Con \(5\) tuổi; mẹ \(30\) tuổi
B. Con \(7\) tuổi; mẹ \(32\) tuổi
C. Con \(10\) tuổi; mẹ \(35\) tuổi
D. Con \(9\) tuổi; mẹ \(39\) tuổi
C. Con \(10\) tuổi; mẹ \(35\) tuổi
- Vì mỗi năm mỗi người tăng thêm 1 tuổi nên hiệu số tuổi không thay đổi. Hiện nay mẹ hơn con \(25\) tuổi thì cách đây \(5\) năm mẹ vẫn hơn con \(25\) tuổi . Từ đây ta đưa được về bài toán dạng tìm hai số khi biết hiệu và tỉ số của hai số.
Ta vẽ sơ đồ biểu diễn tuổi con cách đây \(5\) năm là \(1\) phần, tuổi mẹ cách đây \(5\) năm là \(6\) phần. Coi số tuổi của con là số bé, số tuổi của mẹ là số lớn, ta tìm hai số theo công thức:
Số bé = (Hiệu : hiệu số phần bằng nhau) × số phần của số bé
hoặc
Số lớn = (Hiệu : hiệu số phần bằng nhau) × số phần của số lớn.
- Tìm số tuổi hiện nay của mỗi người ta lấy số tuổi cách đây \(5\) năm cộng thêm \(5\) tuổi.
Vì mỗi năm mỗi người tăng thêm 1 tuổi nên hiệu số tuổi không thay đổi. Do đó, cách đây \(5\) năm mẹ vẫn hơn con \(25\) tuổi.
Ta có sơ đồ tuổi của hai mẹ con cách đây \(5\) năm:
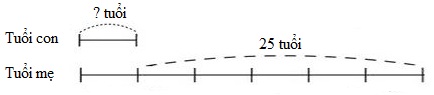
Theo sơ đồ, hiệu số phần bằng nhau là:
\(6 - 1 = 5\) (phần)
Tuổi con cách đây \(5\) năm là:
\(25:5 \times 1 = 5\) (tuổi)
Tuổi con hiện nay là:
\(5 + 5 = 10\) (tuổi)
Tuổi mẹ hiện nay là:
\(10 + 25 = 35\) (tuổi)
Đáp số: Con \(10\) tuổi; mẹ \(35\) tuổi.
 Điền số thích hợp vào ô trống:
Điền số thích hợp vào ô trống:
Hiệu của hai số là \(882\). Số thứ nhất là số tròn chục và nếu xóa đi chữ số \(0\) ở bên phải số thứ nhất thì được số thứ hai.
Vậy số thứ nhất là
, số thứ hai là
Hiệu của hai số là \(882\). Số thứ nhất là số tròn chục và nếu xóa đi chữ số \(0\) ở bên phải số thứ nhất thì được số thứ hai.
Vậy số thứ nhất là
, số thứ hai là
Bài toán cho biết hiệu của hai số là \(882\). Vì số thứ nhất là số tròn chục và nếu xóa đi chữ số \(0\) ở bên phải số thứ nhất thì được số thứ hai nên số thứ nhất gấp 10 lần số thứ hai. Từ đây ta đưa được về bài toán dạng tìm hai số khi biết hiệu và tỉ số của hai số.
Ta vẽ sơ đồ biểu thị số thứ hai là 1 phần, số thứ nhất là 10 phần như thế. Coi số thứ nhất là số lớn, số thứ hai là số bé, ta tìm hai số theo công thức:
Số bé = (hiệu : hiệu số phần bằng nhau) × số phần của số bé
hoặc
Số lớn = (hiệu : hiệu số phần bằng nhau) × số phần của số lớn.
Vì số thứ nhất là số tròn chục và nếu xóa đi chữ số \(0\) ở bên phải số thứ nhất thì được số thứ hai nên số thứ nhất gấp 10 lần số thứ hai.
Ta có sơ đồ:
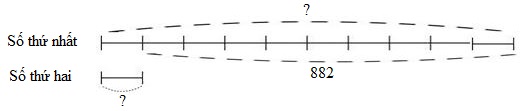
Theo sơ đồ, hiệu số phần bằng nhau là:
\(10 - 1 = 9\) (phần)
Số thứ hai là:
\(882:9 \times 1 = 98\)
Số thứ nhất là:
\(98 \times 10 = 980\)
Đáp số: Số thứ nhất: \(980\);
Số thứ hai: \(98\).
Vậy hai số điền vào ô trống theo thứ tự từ trái qua phải là \(980\,;\,\,98\).
