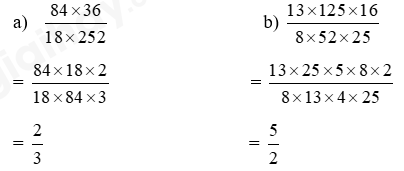Câu 6
Điền dấu >, <, = thích hợp vào chỗ chấm:
Phương pháp giải:
So sánh các số thập phân rồi điền dấu thích hợp vào chỗ chấm.
Lời giải chi tiết:
Câu 7
Viết chữ số thích hợp vào chỗ chấm:
34,….67 < 34,167 231,45 = 231,4…..
12…,321 < 121,321 26,3…6 > 26,386
345,4…5 = 345,…25 461,2…4 < 461,214
Phương pháp giải:
Nếu phần nguyên của hai số đó bằng nhau thì ta so sánh phần thập phân, lần lượt từ hàng phần mười, hàng phần trăm, hàng phần nghìn ... đến cùng một hàng nào đó, số thập phân nào có chữ số ở hàng tương ứng lớn hơn thì số đó lớn hơn.
Lời giải chi tiết:
Câu 8
Tìm số tự nhiên x thỏa mãn:
a) 1,23 < x < 2,13
b) 47,8 > x > 45,6
c) 164,32 < x < 169,9
Phương pháp giải:
Tìm số tự nhiên thỏa mãn yêu cầu của đề bài.
Lời giải chi tiết:
a) 1,23 < x < 2,13
Vậy x = 2
b) 47,8 > x > 45,6
Vậy x = 46 hoặc x = 47
c) 164,32 < x < 169,9
Vậy x = 165 ; 166 ; 167 ; 168 hoặc 169
Câu 9
Tìm số thập phân có một chữ số ở phần thập phân thỏa mãn:
a) 34,12 < x < 34,56
b) 9,86 < x < 9,45
c) 12 < x < 13
Phương pháp giải:
Áp dụng quy tắc so sánh hai số thập phân:
+ So sánh các phần nguyên của hai số đó như so sánh hai số tự nhiên, số thập phân nào có phần nguyên lớn hơn thì số đó lớn hơn.
+ Nếu phần nguyên của hai số đó bằng nhau thì ta so sánh phần thập phân, lần lượt từ hàng phần mười, hàng phần trăm, hàng phần nghìn ...
Lời giải chi tiết:
a) 34,12 < x < 34,56
Vậy x = 34,2 ; 34,3 ; 34,4 hoặc 34,5
b) 9,86 > x > 9,45
Vậy x = 9,8 ; 9,7 ; 9,6 hoặc 9,5
c) 12 < x < 13
Vậy x = 12,1 ; 12,2 ; 12,3 ; 12,4 ; 12,5 ; 12,6 ; 12,7 ; 12,8 ; 12,9
Câu 10
Tìm hai số tự nhiên x, y liên tiếp sao cho:
a) x < 20,3 < y
b) x < 16,78 < y
Phương pháp giải:
Dựa vào cách so sánh số thập phân để tìm giá trị thích hợp của x, y.
Lời giải chi tiết:
a) x < 20,3 < y
Ta có 20 < 20,3 < 21
Vậy x = 20, y = 21
b) x < 16,78 < y
Ta có 16 < 16,78 < 17
Vậy x = 16, y = 17
Câu 11
Tính bằng cách thuận tiện:
a) $\frac{{84 \times 36}}{{18 \times 252}}$
b) $\frac{{13 \times 125 \times 16}}{{8 \times 52 \times 25}}$
Phương pháp giải:
Tách tích ở tử số thành tích của các thừa số, sau đó lần lượt chia tử số và mẫu số cho các thừa số chung.
Lời giải chi tiết: