|
Bài 1: Một quả bóng được tăng tốc dưới tác dụng của trọng lực khi lăn xuống dọc một mặt phẳng nghiêng cố định. Động lượng của quả bóng có được bảo toàn trong quá trình này không? Giải thích. |
Phương pháp giải:
Nếu không có ngoại lực nào tác dụng lên hệ hoặc tổng tất cả các ngoại lực bằng 0 thì tổng động lượng của hệ không đổi, tức là động lượng được bảo toàn.
Lời giải chi tiết:
Quả bóng chịu tác dụng của trọng lực lăn xuống mặt phẳng nghiêng, tổng tất cả các ngoại lực của quả bóng khác 0 nên động lượng của quả bóng không được bảo toàn.
|
Bài 2: Xác định động lượng trong các trường hợp sau: a) Con dê có khối lượng 60 kg đang chuyển động về hướng đông với vận tốc 9 m/s. b) Ô tô khối lượng 1000 kg chuyển động theo hướng bắc với vận tốc 20 m/s. c) Một người có khối lượng 40 kg đang chuyển động về hướng nam với vận tốc 2 m/s. |
Phương pháp giải:
Biểu thức tính động lượng: p = m.v
Trong đó:
+ p: động lượng của vật (kg.m/s)
+ m: khối lượng của vật (kg).
+ v: tốc độ của vật (m/s).
Lời giải chi tiết:
a) Động lượng của con dê là: p = m.v = 60.9 = 540 (kg.m/s).
b) Động lượng của ô tô là: p = m.v = 1000.20 = 2.104 (kg.m/s).
c) Động lượng của người là: p = m.v = 40.2 = 80 (kg.m/s).
|
Bài 3. Một quả cầu khối lượng 2 kg, chuyển động với tốc độ 3,0 m/s, đập vuông góc vào tường và bị bật ngược trở lại với cùng tốc độ. So sánh động lượng và động ănn của quả cầu trước và sau va chạm. |
Phương pháp giải:
Biểu thức tính động lượng: p = m.v
Biểu thức tính động năng là: \({W_d} = \frac{1}{2}m{v^2}\)
Lời giải chi tiết:
Chọn chiều dương là chiều chuyển động của quả cầu đập vào tường
Động lượng của quả cầu trước va chạm: p = m.v = 2.3,0 = 6,0 (kg.m/s)
Động lượng của quả cầu sau va chạm: p’ = -m.v’ = -2,3,0 = -6,0 (kg.m/s)
=> Động lượng của quả cầu sau va chạm giảm
Động năng của quả cầu trước va chạm là: \({W_d} = \frac{1}{2}m{v^2} = \frac{1}{2}.2.{(3,0)^2} = 9,0(J)\)
Động năng của quả cầu sau va chạm là: \(W_d^; = \frac{1}{2}mv{'^2} = \frac{1}{2}.2.{( - 3,0)^2} = 9,0(J)\)
=> Động năng không thay đổi
|
Bài 4: Một ô tô khối lượng 900 kg khởi hành từ trạng thái nghỉ có gia tốc không đổi là 3,5 m/s2 . Tính động lượng của ô tô sau khi nó đi được quãng đường 40 m |
Phương pháp giải:
Biểu thức tính động lượng: p = m.v
Trong đó m là khối lượng của vật (kg); v là vận tốc của vật (m/s).
Mối liên hệ giữa quãng đường, gia tốc và vận tốc là: \({v^2} - v_0^2 = 2as\)
Lời giải chi tiết:
Vật khởi hành từ trạng thái nghỉ nên vận tốc ban đầu v0 = 0.
Vận tốc của ô tô khi đi được quãng đường 40 m là: \(v = \sqrt {2as} = \sqrt {2.3,5.40} = 2\sqrt {70} (m/s)\)
Động lượng của ô tô là: \(p = m.v = 900.2\sqrt {70} \approx 15060(kg.m/s)\)
|
Bài 5. Một quả bóng bida khối lượng 0,35 kg va chạm vuông góc vào mặt bên của mặt bida và bật ra cũng vuông góc. Tốc độ của nó trước khi va chạm là 2,8 m/s và tốc độ sau khi va chạm là 2,5 m/s. Tính độ thay đổi động lượng của quả bida. |
Phương pháp giải:
Biẻu thức tính độ thay đổi động lượng: \(\Delta p = \left| {{p_s} - {p_{tr}}} \right| = \left| {m.{v_s} - m.{v_{tr}}} \right|\)
Lời giải chi tiết:
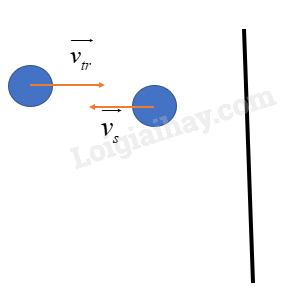
Độ thay đổi động lượng của quả bida là:
\(\Delta p = \left| {{p_s} - {p_{tr}}} \right| = \left| {m.{v_s} - m.{v_{tr}}} \right| = \left| {0,25(2,5 - 2,8)} \right| = 0,075(kg.m/s)\)
|
Bài 6. Một quả bóng gôn có khối lượng 0,046 kg. Vận tốc của quả bóng ngay sau khi rời khỏi gậy gôn là 50 m/s. Gậy đánh gôn tiếp xúc với bóng trong thời gian 1,3 mili giây. Tính lực trung bình do gậy đánh gôn tác dụng lên quả bóng. |
Phương pháp giải:
Mối liên hệ giữa độ biến thiên động lượng, lực tác dụng và thời gian là: \(\Delta p = F.\Delta t\)
Lời giải chi tiết:
Lực trung bình do gậy đánh gôn tác dụng lên quả bóng là:
\(F = \frac{{\Delta p}}{{\Delta t}} = \frac{{m.\Delta v}}{{\Delta t}} = \frac{{0,046.50}}{{1,{{3.10}^{ - 3}}}} \approx 1769,23(N)\)
