Đề bài
Cho đường tròn (O) đường kính AB và cung AC có số đo nhỏ hơn 90o. Vẽ dây CD vuông góc với AB và vẽ dây DE song song với AB. Chứng minh rằng:
a) cung AC= cung BE
b) Ba điểm C, O, E thẳng hàng.
Phương pháp giải - Xem chi tiết
a) Chứng minh cung AC và cung BE cùng bằng cung AD.
b) Chứng minh \(\widehat {CDE} = {90^0} \Rightarrow \widehat {CDE}\) nội tiếp chắn nửa đường tròn.
Lời giải chi tiết
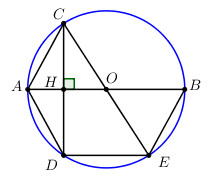
a) Ta có: AB // DE nên cung AD=cung BE (hai cung giữa 2 dây song song).
Gọi \(H = AB \cap CD\). Vì \(AB \bot CD \) \(\Rightarrow H\) là trung điểm của CD (quan hệ vuông góc giữa đường kính và dây cung).
\( \Rightarrow AB\) là trung trực của của CD \( \Rightarrow AC = AD\) (điểm thuộc trung trực của đoạn thẳng thì cách đều 2 đầu mút của đoạn thẳng đó).
Cung AC=cung AD (2 dây bằng nhau căng 2 cung bằng nhau).
Vậy cung AC=cung BE.
b) Ta có : DE // AB. Mà \(AB \bot CD \Rightarrow BE \bot CD \Rightarrow \widehat {CDE} = {90^0}\) \( \Rightarrow \widehat {CDE}\) nội tiếp chắn nửa đường tròn \( \Rightarrow CE\) là đường kính của đường tròn \(\left( O \right)\).
Vậy C, O, E thẳng hàng.
soanvan.me
