Đề bài
Cho tam giác ABC. Hãy trình bày cách xác định vị trí của điểm M trong tam giác ABC sao cho \(\widehat {MAB} = \widehat {MBC} = \widehat {MCA}\).
Phương pháp giải - Xem chi tiết
Sử dụng định lí: Trong 1 đường tròn, góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn 1 cung thì bằng nhau.
Lời giải chi tiết
Giả sử dựng được điểm M thỏa mãn điều kiện đề bài.
Ta có: \(\widehat {MAB} = \widehat {MBC} \Rightarrow BC\) là tiếp tuyến của đường tròn ngoại tiếp tam giác AMB.
Chứng minh tương tự ta có CA là tiếp tuyến của đường tròn ngoại tiếp tg BMC.
Suy ra cách dựng điểm M như sau:
- Dựng đường tròn \(\left( {{O_1}} \right)\) qua A; B tiếp xúc với BC tại B (\({O_1}\) là giao điểm của đường thẳng đi qua B và vuông góc với BC và đường thẳng trung trực của đoạn AB)
- Dựng đường tròn \(\left( {{O_2}} \right)\) qua B, C và tiếp xúc với CA tai C (\({O_2}\) là giao điểm của đường thẳng đi qua C và vuông góc với AC và đường thẳng trung trực của đoạn BC)
- M là giao điểm của \(\left( {{O_1}} \right)\) và \(\left( {{O_2}} \right)\).
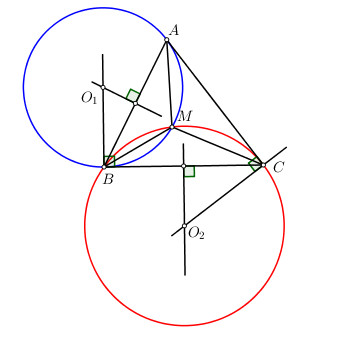
* Chứng minh:
Xét đường tròn \(\left( {{O_1}} \right)\) có \(\widehat {MAB} = \widehat {MBC}\) (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung MB).
Xét đường tròn \(\left( {{O_2}} \right)\) có \(\widehat {MBC} = \widehat {MCA}\) (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung MC).
Vậy \(\widehat {MAB} = \widehat {MBC} = \widehat {MCA}\)
soanvan.me
