Đề bài
Cho hình chữ nhật ABCD với AB = \(2\sqrt 3 \)cm, BC = 2 cm và đường tròn ngoại tiếp (O)
a) Tính diện tích hình tròn (O)
b)Tính tổng diện tích của bốn hình viên phân
c) Tính diện tích hình viên phân BC .
Phương pháp giải - Xem chi tiết
a) Áp dụng định lí Pytago trong tam giác vuông ABC tính AC và suy ra bán kính đường tròn \(\left( O \right)\). Sử dụng công thức tính diện tích hình tròn \(S = \pi {R^2}\).
b) Tổng diện tích 4 hình viên phân bằng diện tích hình tròn trừ diện tích hình chữ nhật ABCD.
c) Diện tích hình viên phân BC bằng diện tích hình quạt OBC trừ diện tích tam giác OBC.
Sử dụng công thức tính diện tích hình quạt \(S = \dfrac{{\pi {R^2}n}}{{360}}\).
Lời giải chi tiết
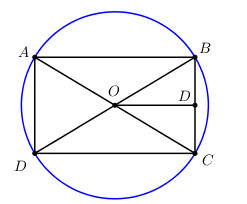
a) Áp dụng định lí Pytago trong tam giác vuông ABC có:
\(A{C^2} = A{B^2} + B{C^2} = {\left( {2\sqrt 3 } \right)^2} + {2^2} = 16 \)
\(\Rightarrow AC = 4\).
\( \Rightarrow R = OA = OB = OC = OD = \dfrac{1}{2}AC = 2\).
Vậy diện tích hình tròn (O) là: \(S = \pi {R^2} = 4\pi \approx 12,56\,\,\left( {c{m^2}} \right)\).
b) Ta có: \({S_{ABCD}} = AB.BC = 2\sqrt 3 .2 = 4\sqrt 3 \,\,\left( {c{m^2}} \right)\)
Vậy tổng diện tích 4 hình viên phân là \(S' = S - {S_{ABCD}} \approx 5,63\,\,\,\left( {c{m^2}} \right)\)
c) Xét tam giác OBC có \(OB = OC = BC = 2 \Rightarrow \Delta OBC\) đều \( \Rightarrow \widehat {OBC} = {60^0}\)
Suy ra diện tích hình quạt OBC là: \({S_q} = \dfrac{{\pi {R^2}n}}{{360}} = \dfrac{{\pi {{.2}^2}.60}}{{360}} = \dfrac{{2\pi }}{3}\,\,\left( {c{m^2}} \right)\)
Gọi D là trung điểm của BC \( \Rightarrow OD \bot BC\) (quan hệ vuông góc giữa đường kính và dây cung).
Xét tam giác ABC có:
O là trung điểm của AC (gt);
D là trung điểm của BC (theo cách dựng);
\( \Rightarrow OD\) là đường trung bình của tam giác ABC \( \Rightarrow OD = \dfrac{1}{2}AB = \sqrt 3 \).
Ta có: \({S_{\Delta OBC}} = \dfrac{1}{2}OD.BC = \dfrac{1}{2}.\sqrt 3 .2 = \sqrt 3 \,\,\left( {c{m^2}} \right)\)
Vậy diện tích hình viên phân BC bằng \({S_q} - {S_{\Delta OBC}} = \dfrac{{2\pi }}{3} - \sqrt 3 \approx 0,36\,\,\left( {c{m^2}} \right)\)
soanvan.me
