Đề bài
Quan sát hình lập phương \(ABCD.{A_1}{B_1}{C_1}{D_1}\) (h.105)
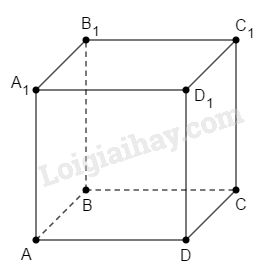
a) Đường thẳng \(A_1B_1\) song song với những mặt phẳng nào?
b) Liệu đường thẳng \(AC\) có song song với mặt phẳng \((A_1C_1B_1)\) hay không?
Phương pháp giải - Xem chi tiết
Sử dụng:
- Hình lập phương là hình hộp chữ nhật có \(6\) mặt đều là hình vuông.
- Khi đường thẳng \(d\) không nằm trong mặt phẳng \((ABCD)\) mà \(d\) song song với đường thẳng của mặt phẳng này thì ta nói đường thẳng \(d\) song song với mặt phẳng \((ABCD)\).
Lời giải chi tiết
a) \(ABCD.{A_1}{B_1}{C_1}{D_1}\) là hình lập phương nên \(A_1B_1 BA; A_1B_1C_1D_1\) là các hình vuông.
Có \(A_1B_1// AB\) (vì \(A_1B_1 BA\) là hình vuông) nên \(A_1B_1// mp(ABCD)\).
Có \(A_1B_1// C_1D_1\) (vì \(A_1B_1C_1D_1\) là hình vuông) nên \(A_1B_1 // mp(CDD_1C_1)\).
b) \(ABCD.{A_1}{B_1}{C_1}{D_1}\) là hình lập phương nên \(AA_1//CC_1;AA_1=CC_1\) do đó \(AA_1C_1C\) là hình bình hành.
Suy ra \(AC // A_1C_1\) (tính chất hình bình hành).
Ta có \(AC // A_1C_1\) mà \(AC\) không thuộc \(mp(A_1C_1B_1)\) nên \(AC // mp(A_1C_1B_1)\).
soanvan.me
