Xét chiều biến thiên của các hàm số sau:
LG a
\(y = {1 \over x} - {1 \over {x - 2}}\)
Lời giải chi tiết:
TXĐ: \(D = \mathbb{R}\backslash \left\{ {0;2} \right\}\)
Ta có:
\(\begin{array}{l}y = \frac{{x - 2 - x}}{{x\left( {x - 2} \right)}} = \frac{{ - 2}}{{{x^2} - 2x}}\\y' = \frac{2({2x - 2})}{{{{\left( {{x^2} - 2x} \right)}^2}}}\\y' = 0 \Leftrightarrow 2x - 2 = 0 \Leftrightarrow x = 1\end{array}\)
Bảng xét dấu:
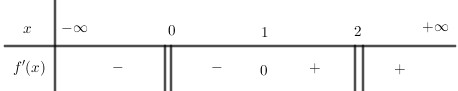
Hàm số nghịch biến trên mỗi khoảng \(\left( { - \infty ;0} \right)\) và \(\left( {0;1} \right)\), đồng biến trên mỗi khoảng \(\left( {1;2} \right)\) và \(\left( {2; + \infty } \right)\)
LG b
\(y = {3x \over {{x^2} + 1}}\)
Lời giải chi tiết:
TXĐ: \(D = \mathbb{R}\)
Ta có:
\(y' = \frac{{3\left( {{x^2} + 1} \right) - 3x.2x}}{{{{\left( {{x^2} + 1} \right)}^2}}}\) \( = \frac{{ - 3{x^2} + 3}}{{{{\left( {{x^2} + 1} \right)}^2}}}\)
\(y' > 0 \Leftrightarrow - 3{x^2} + 3 > 0\) \( \Leftrightarrow - 1 < x < 1\)
Nên hàm số đồng biến trên khoảng \(\left( { - 1;1} \right)\).
\(y' < 0 \Leftrightarrow - 3{x^2} + 3 < 0\) \( \Leftrightarrow \left[ \begin{array}{l}x > 1\\x < - 1\end{array} \right.\)
Nên hàm số nghịch biến trên các khoảng \(\left( { - \infty ; - 1} \right)\) và \(\left( {1; + \infty } \right)\).
Hàm số nghịch biến trên mỗi khoảng \(\left( { - \infty ; - 1} \right)\) và \(\left( {1; + \infty } \right)\), đồng biến trên khoảng \(\left( { - 1;1} \right)\)
LG c
\(y = {{x + 1} \over {3\sqrt x }}\)
Lời giải chi tiết:
TXĐ: \(D = \left( {0; + \infty } \right)\).
Ta có:
\(\begin{array}{l}y' = \frac{1}{3}.\frac{{\sqrt x - \left( {x + 1} \right).\frac{1}{{2\sqrt x }}}}{x}\\ = \frac{1}{3}.\frac{{2x - x - 1}}{{2\sqrt x }} = \frac{{x - 1}}{{6\sqrt x }}\end{array}\)
\(y' > 0 \Leftrightarrow x > 1\) nên hàm số đồng biến trong khoảng \(\left( {1; + \infty } \right)\).
\(y' < 0 \Leftrightarrow 0 < x < 1\) nên hàm số nghịch biến trong khoảng \(\left( {0;1} \right)\).
Hàm số nghịch biến trên khoảng \(\left( {0;1} \right)\) và đồng biến trên khoảng \(\left( {1; + \infty } \right)\)
LG d
\(y=\sqrt {{x^2} + 2x + 3} \)
Lời giải chi tiết:
TXĐ: \(D = \mathbb{R}\).
Ta có: \(y' = \frac{{2x + 2}}{{2\sqrt {{x^2} + 2x + 3} }}\) \( = \frac{{x + 1}}{{\sqrt {{x^2} + 2x + 3} }}\)
\(y' > 0 \Leftrightarrow x > - 1\) nên hàm số đồng biến trong \(\left( { - 1; + \infty } \right)\).
\(y' < 0 \Leftrightarrow x < - 1\) nên hàm số nghịch biến trong \(\left( { - \infty ; - 1} \right)\).
Hàm số nghịch biến trên khoảng \(\left( { - \infty ; - 1} \right)\) và đồng biến trên khoảng \(\left( { - 1; + \infty } \right)\).
soanvan.me
