Xét chiều biến thiên các hàm số sau:
LG a
\(f(x) = {1 \over 2}{x^4} + {x^3} - x + 5\)
Lời giải chi tiết:
TXĐ: \(D = \mathbb{R}\).
\(f'\left( x \right) = 2{x^3} + 3{x^2} - 1\)
\(\begin{array}{l}
= 2{x^3} + 2{x^2} + {x^2} - 1\\
= 2{x^2}\left( {x + 1} \right) + \left( {x - 1} \right)\left( {x + 1} \right)\\
= \left( {x + 1} \right)\left( {2{x^2} + x - 1} \right)\\
= \left( {x + 1} \right)\left( {2{x^2} + 2x - x - 1} \right)\\
= \left( {x + 1} \right)\left[ {2x\left( {x + 1} \right) - \left( {x + 1} \right)} \right]\\
= {\left( {x + 1} \right)^2}\left( {2x - 1} \right)
\end{array}\)
\(f'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = \frac{1}{2}\end{array} \right.\)
BXD:
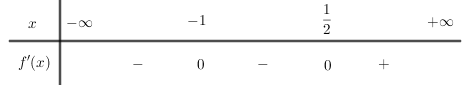
Hàm số nghịch biến trên khoảng \(\left( { - \infty ;{1 \over 2}} \right)\) và đồng biến trên khoảng \(\left( {{1 \over 2}; + \infty } \right)\)
LG b
\(f(x) = {3 \over 4}{x^4} - 2{x^3} + {3 \over 2}{x^2} - 6x + 11\)
Lời giải chi tiết:
TXĐ: \(D = \mathbb{R}\).
\(\begin{array}{l}f'\left( x \right) = 3{x^3} - 6{x^2} + 3x - 6\\ = 3\left( {{x^3} - 2{x^2} + x - 2} \right)\\ = 3\left[ {{x^2}\left( {x - 2} \right) + \left( {x - 2} \right)} \right]\\= 3\left( {x - 2} \right)\left( {{x^2} + 1} \right)\end{array}\)
\(f'\left( x \right) > 0 \Leftrightarrow x > 2\) nên hàm số đồng biến trên \(\left( {2; + \infty } \right)\).
\(f'\left( x \right) < 0 \Leftrightarrow x < 2\) nên hàm số nghịch biến trên \(\left( { - \infty ;2} \right)\).
Hàm số nghịch biến trên khoảng \(\left( { - \infty ;2} \right)\) và đồng biến trên khoảng \(\left( {2; + \infty } \right)\)
LG c
\(f(x) = {x^3} - {4 \over 5}{x^5} + 8\)
Lời giải chi tiết:
TXĐ: \(D = \mathbb{R}\).
\(f'\left( x \right) = 3{x^2} - 4{x^4}\) \( = {x^2}\left( {3 - 4{x^2}} \right)\)
\(\begin{array}{l}f'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}{x^2} = 0\\3 - 4{x^2} = 0\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = \pm \frac{{\sqrt 3 }}{2}\end{array} \right.\end{array}\)
BXD:
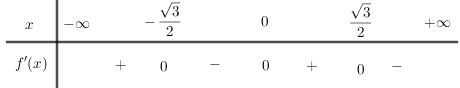
Hàm số nghịch biến trên mỗi khoảng \(\left( { - \infty ;{{\sqrt 3 } \over 2}} \right)\) và \(\left( {{{\sqrt 3 } \over 2}; + \infty } \right)\), đồng biến trên khoảng \(\left( { - {{\sqrt 3 } \over 2};{{\sqrt 3 } \over 2}} \right)\)
LG d
\(f(x) = 9{x^7} - 7{x^6} + {7 \over 5}{x^5} + 12\)
Lời giải chi tiết:
TXĐ: \(D = \mathbb{R}\)
\(\begin{array}{l}f'\left( x \right) = 63{x^6} - 42{x^5} + 7{x^4}\\ = 7{x^4}\left( {9{x^2} - 6x + 1} \right)\\ = 7{x^4}{\left( {3x - 1} \right)^2} \ge 0,\forall x \in \mathbb{R}\end{array}\)
Vậy hàm số đồng biến trên \(\mathbb{R}\).
soanvan.me
