Cho hàm số \(y = \displaystyle{3 \over 4}{x^2}\)
LG a
Vẽ đồ thị của hàm số.
Phương pháp giải:
+) Vẽ đồ thị: Lấy một số điểm thuộc đồ thị hàm số, rồi từ đó vẽ đồ thị.
Lời giải chi tiết:
Vẽ đồ thị hàm số \(y = \displaystyle{3 \over 4}{x^2}\)
Ta có bảng giá trị
|
\(x\) |
\(-2\) |
\(-1\) |
\(0\) |
\(1\) |
\(3\) |
| \(y = \displaystyle{3 \over 4}{x^2}\) |
\(3\) |
\(\displaystyle{3 \over 4}\) |
\(0\) |
\(\displaystyle{3 \over 4}\) |
\(2\) |
Vẽ đồ thị:
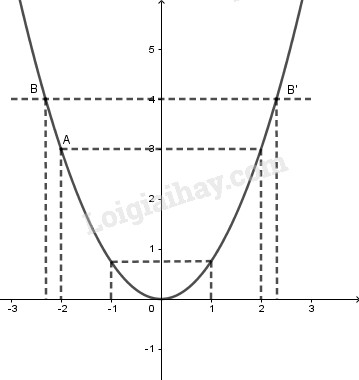
LG b
Tìm trên đồ thị điểm \(A\) có hoành độ bằng \(-2.\) Bằng đồ thị, tìm tung độ của \(A.\)
Phương pháp giải:
+) Từ tọa độ đã biết trên đồ thị ta vẽ các đường thẳng song song với hai trục rồi xác định được tọa độ giao điểm.
Lời giải chi tiết:
Từ điểm \(x = -2\) kẻ đường thẳng song song với trục tung cắt đồ thị tại \(A.\)
Từ \(A\) kẻ đường thẳng song song với trục hoành cắt trục tung tại điểm có tung độ \(y = 3;\)\( A (-2; 3)\)
LG c
Tìm trên đồ thị các điểm có tung độ bằng \(4.\) Tính gần đúng (làm tròn đến chữ số thập phân thứ nhất) hoành độ của những điểm này bằng hai cách:
- Ước lượng trên đồ thị;
- Tính theo công thức \(y = \displaystyle{3 \over 4}{x^2}\)
Phương pháp giải:
Từ tọa độ đã biết trên đồ thị ta vẽ các đường thẳng song song với hai trục rồi xác định được tọa độ giao điểm.
Lời giải chi tiết:
Từ điểm có tung độ \(y = 4\) kẻ đường thẳng song song với trục hoành cắt đồ thị tại \(B\) và \(B’\) là điểm có tung độ \(y = 4.\)
Từ \(B\) và \(B’\) kẻ đường thẳng song song với trục tung cắt trục hoành tại điểm có hoành độ \(x \approx - 2,3;x \approx 2,3\)
Thay \(y = 4\) ta có: \(4 =\displaystyle {3 \over 4}{x^2} \Leftrightarrow {x^2} =\displaystyle {{16} \over 3} \)\(\Leftrightarrow x =\displaystyle \pm {{4\sqrt 3 } \over 3} \approx \pm 2,3\)
soanvan.me
