Cho hàm số \(y = f\left( x \right) = - 1,5{x^2}\)
LG a
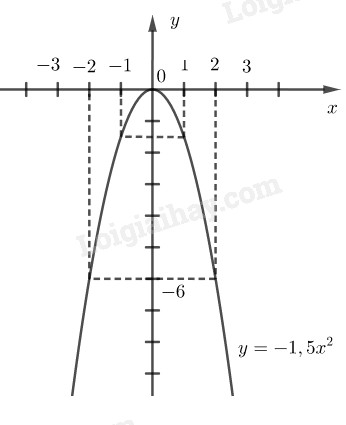
Vẽ đồ thị của hàm số.
Phương pháp giải:
+) Vẽ đồ thị: Lấy một số điểm thuộc đồ thị rồi từ đó vẽ đồ thị.
Lời giải chi tiết:
Vẽ đồ thị hàm số \(y = f\left( x \right) = - 1,5{x^2}\)
|
\(x\) |
\(-2\) |
\(-1\) |
\(0\) |
\(1\) |
\(2\) |
| \(y = f\left( x \right) = - 1,5{x^2}\) |
\(-6\) |
\(-1,5\) |
\(0\) |
\(-1,5\) |
\(-6\) |
LG b
Không làm tính, dùng đồ thị để so sánh \(f(-1,5)\) và \(f(-0,5),\) \(f(0,75)\) và \(f(1,5).\)
Phương pháp giải:
+) Nếu \(a<0\) thì hàm số đồng biến khi \(x<0\) và nghịch biến khi \(x>0\).
Lời giải chi tiết:
Cách 1: Hàm số \(y = - 1,5{x^2}\) có \(a = - 1,5 < 0\)
Suy ra hàm số đồng biến khi \(x < 0,\) nghịch biến khi \(x > 0\)
Từ đó:
+) Vì \(-1,5<-0,5<0\)\( \Rightarrow f\left( { - 1,5} \right) < f\left( { - 0,5} \right)\)
+) Vì \(0<0,75<1,5\) \(\Rightarrow f\left( {0,75} \right) > f\left( {1,5} \right)\)
Cách 2: Quan sát đồ thị hàm số để so sánh.
Ta được: \(f\left( { - 1,5} \right) < f\left( { - 0,5} \right)\)
\(f\left( {0,75} \right) > f\left( {1,5} \right)\)
LG c
Dùng đồ thị, tìm những giá trị thích hợp điền vào các chỗ \((…):\)
Khi \(1\le x\le 2\) thì \(... ≤ y ≤ …\)
Khi \(-2 ≤ x ≤ 0\) thì \(…≤ y ≤ …\)
Khi \(-2 ≤ x ≤ 1\) thì \(… ≤ y ≤ …\)
Phương pháp giải:
Nhìn đồ thị hàm số để điền vào chỗ trống.
Lời giải chi tiết:
Từ đồ thị, ta có: \(y(1)=-1,5;y(2)=-6;\)\(y(-2)=-6;y(0)=0\). Do đó:
Khi \(1 \le x \le 2\) thì \(-6 ≤ y ≤ -1,5\)
Khi \(-2 ≤ x ≤ 0\) thì \(-6 ≤ y ≤ 0\)
Khi \(-2 ≤ x ≤ 1\) thì \(-6 ≤ y ≤ 0\)
soanvan.me
