Đề bài
Cho hình thang cân \(ABCD \;(AB // CD)\), \(E\) là giao điểm của hai đường chéo. Chứng minh rằng \(EA = EB, EC = ED.\)
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
- Hình thang cân có hai cạnh bên bằng nhau, hai đường chéo bằng nhau.
- Hai tam giác bằng nhau có các góc tương ứng bằng nhau
- Tam giác cân có hai cạnh bên bằng nhau, hai góc đáy bằng nhau.
Lời giải chi tiết
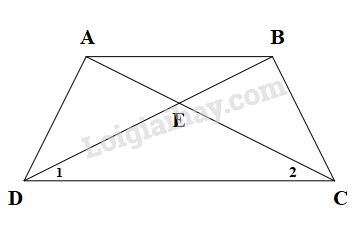
Do \(ABCD\) là hình thang cân (giả thiết) nên \(AD = BC, AC = BD\) (tính chất hình thang cân)
Xét \(\Delta A{\rm{D}}C\) và \(\Delta B{\rm{C}}D\)
+) \(AD = BC\) (chứng minh trên)
+) \(AC = BD\) (chứng minh trên)
+) \(DC\) chung
Suy ra \(∆ADC = ∆BCD\) (c.c.c)
Suy ra \(\widehat{C_{2}}=\widehat{D_{1}}\) (\(2\) góc tương ứng)
Do đó \(\Delta E{\rm{D}}C\) cân tại \(E\) (dấu hiệu nhận biết tam giác cân)
\( \Rightarrow EC = E{\rm{D}}\) (tính chất tam giác cân)
Lại có:
\(AC = B{\rm{D}}\left( \text{chứng minh trên} \right)\)
\(EC = E{\rm{D}}\left( \text{chứng minh trên} \right)\)
Trừ vế với vế, ta được \( AC - CE= B{\rm{D}} - DE\)
Hay \( E{\rm{A}} = EB\).
Vậy \(EA = EB, EC = ED.\)
soanvan.me
