Video hướng dẫn giải
Cho ba đoạn thẳng có độ dài là \(m,n,p\) ( cùng đơn vị đo).
Dựng đoạn thẳng có độ dài \(x\) sao cho:
LG a.
\(\dfrac{x}{m} =2\);
Phương pháp giải:
Áp dụng hệ quả của định lý TaLet.
Giải chi tiết:
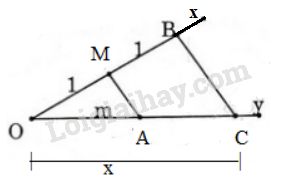
Cách dựng:
- Vẽ hai tia \(Ox, Oy\) không đối nhau.
- Trên tia \(Ox\) lấy hai điểm \(M,\,B\) sao cho \(OM =1;OB=2\) đơn vị.
- Trên tia \(Oy\) lấy điểm A sao cho \(OA=m\)
- Nối \(MA\).
- Vẽ đường thẳng đi qua \(B\) và song song với \(MA\) cắt \(Oy\) tại \(C\) thì \(OC=x\) là đoạn thẳng cần dựng.
Chứng minh:
Xét tam giác OBC có \(MN//BC\) nên:
\(\dfrac{OC}{OA} = \dfrac{OB}{OM}\) (theo hệ quả định lí Talet)
\( \Rightarrow \dfrac{x}{m} = 2\)
LG b.
\(\dfrac{x}{n}= \dfrac{2}{3}\);
Phương pháp giải:
Áp dụng hệ quả của định lý TaLet.
Giải chi tiết:
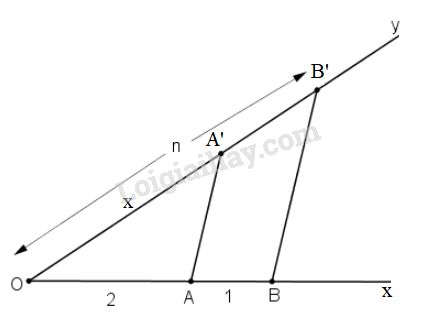
Cách dựng:
- Vẽ hai tia \(Ox\) và \(Oy\) không đối nhau.
- Trên tia \(Ox\) đặt hai đoạn \(OA= 2\) đơn vị, \(OB= 3\) đơn vị.
- Trên tia \(Oy\) đặt đoạn \(OB' = n\)
- Nối \(BB'\)
- Vẽ đường thẳng qua \(A\) song song với \(BB'\) cắt \(Oy\) tại \(A'\) và đặt \(OA' = x\).
Khi đó OA' là đoạn thẳng cần dựng.
Chứng minh:
Xét tam giác OBB' có: \(AA' // BB'\)
\(\Rightarrow \dfrac{OA'}{OB'} = \dfrac{OA}{OB}\) (theo hệ quả định lí Talet)
hay \(\dfrac{x}{n} = \dfrac{2}{3}\)
LG c.
\(\dfrac{m}{x} = \dfrac{n}{p}\)
Phương pháp giải:
Áp dụng hệ quả của định lý TaLet.
Giải chi tiết:
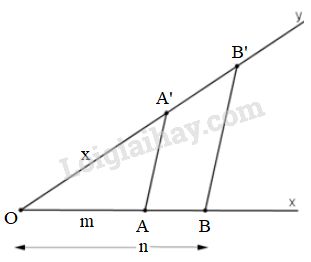
Cách dựng:
- Vẽ tia \(Ox, Oy\) không đối nhau.
- Trên tia \(Ox\) đặt đoạn \(OA= m, OB= n\).
- Trên tia \(Oy\) đặt đoạn \(OB' = p\).
- Vẽ đường thẳng qua \(A\) và song song với \(BB'\) cắt \(Oy\) tại \(A'\) thì \(OA' = x\) là đoạn thẳng cần dựng.
Chứng minh:
Xét tam giác OBB' có \(AA' // BB'\)
\(\Rightarrow \dfrac{OA}{OA'} = \dfrac{OB}{OB'}\) (theo hệ quả định lí Talet) hay \(\dfrac{m}{x} = \dfrac{n}{p}\)
soanvan.me
