Đề bài
Cho tam giác \(ABC\) và điểm \(D\) trên cạnh \(AB\) sao cho \(AD= 13,5cm, DB= 4,5cm\). Tính tỉ số các khoảng cách từ điểm \(D\) và \(B\) đến cạnh \(AC\).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Áp dụng: Hệ quả của định lý TaLet.
Lời giải chi tiết
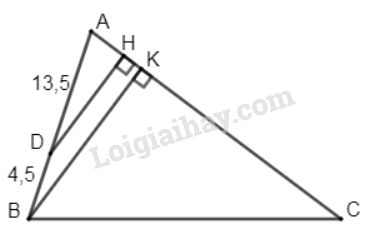
Gọi \(DH\) và \(BK\) lần lượt là khoảng cách từ \(B\) và \(D\) đến cạnh \(AC\).
Ta có \(DH // BK\) (vì cùng vuông góc với \(AC\))
\( \Rightarrow \dfrac{DH}{BK} = \dfrac{AD}{AB}\) (theo hệ quả định lý Ta Let)
Mà \(AB = AD + DB\) (giả thiết)
\( \Rightarrow AB = 13,5 + 4,5 = 18\) (cm)
Vậy \(\dfrac{DH}{BK} = \dfrac{13,5}{18} = \dfrac{3}{4}\)
Vậy tỉ số khoảng cách từ điểm \(D\) và \(B\) đến \(AC\) bằng \(\dfrac{3}{4}\)
soanvan.me
