Đề bài
Cho tam giác \(ABC.\) Lấy các điểm \(D,\, E\) theo thứ tự trên các cạnh \(AB,\, AC\) sao cho \(BD = CE.\) Gọi \(M,\, N,\, I,\, K\) theo thứ tự là trung điểm của \(BE,\, CD,\, DE,\, BC.\) Chứng minh rằng \(IK\) vuông góc với \(MN.\)
Phương pháp giải - Xem chi tiết
Vận dụng kiến thức :
- Hai đường chéo của hình thoi vuông góc với nhau tại trung điểm của mỗi đường.
- Tính chất đường trung bình của tam giác: Đường trung bình của tam giác song song với cạnh thứ ba và bằng nửa cạnh ấy.
- Chứng minh \(MKNI\) là hình bình hành có hai cạnh kề bằng nhau nên là hình thoi.
Lời giải chi tiết
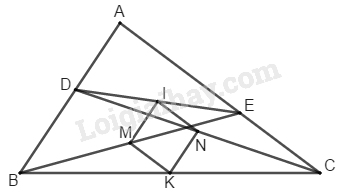
Trong \(∆ BCD\) ta có:
\(K\) là trung điểm của \(BC\) (gt)
\(N\) là trung điểm của \(CD\) (gt)
nên \(NK\) là đường trung bình của \(∆ BCD\)
\(⇒ NK // BD\) và \(NK =\displaystyle {1 \over 2}BD\) (1)
Trong \(∆ BED\) ta có:
\(M\) là trung điểm của \(BE\) (gt)
\(I\) là trung điểm của \(DE\) (gt)
nên \(MI\) là đường trung bình của \(∆ BED\)
\(⇒ MI // BD\) và \(MI =\displaystyle {1 \over 2}BD\) (tính chất đường trung bình của tam giác) (2)
Từ (1) và (2) suy ra: \(MI // NK\) và \(MI = NK\)
nên tứ giác \(MKNI\) là hình bình hành
Trong \(∆ BEC\) ta có:
\(M\) là trung điểm của \(BE\) (gt)
\(K\) là trung điểm của \(BC\) (gt)
Nên \(MK\) là đường trung bình
Suy ra \(MK = \displaystyle {1 \over 2}CE\) (tính chất đường trung bình của tam giác)
Mà \(NK =\displaystyle {1 \over 2}BD\) (theo (1)) và \(BD = CE\) (gt)
Suy ra: \(MK = KN\)
Vây hình bình hành \(MKNI\) là hình thoi.
\(⇒ IK ⊥ MN\) (tính chất hình thoi)
soanvan.me
