Đề bài
Dựng hình thoi \(ABCD,\) biết cạnh bằng \(2\,cm,\) một đường chéo bằng \(3\,cm.\)
Phương pháp giải - Xem chi tiết
- Dựng tam giác \(ABD\) có hai cạnh bằng \(2\,cm\) và cạnh đáy bằng độ dài đường chéo của hình thoi.
- Ở mặt phẳng đối diện, vẽ một tam giác chung cạnh đáy và độ dài cạnh bên bằng \(2\,cm.\)
- Chứng minh hình vừa dựng được thỏa mãn điều kiện bài toán.
Lời giải chi tiết
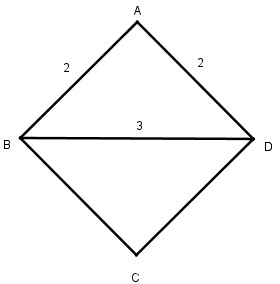
Cách dựng:
- Dựng \(∆ ABD\) biết \(AB = AD = 2\,(cm),\) \(BD = 3cm\)
- Trên nửa mặt phẳng bờ \(BD\) không chứa điểm \(A.\) Từ \(B\) dựng tia \(Bx // AD,\) từ \(D\) dựng tia \(Dy // AB,\) chúng cắt nhau tại \(C.\)
Ta có hình thoi \(ABCD\) cần dựng
Chứng minh:
Vì \(AB // CD\) và \(AD // BC\) nên tứ giác \(ABCD\) là hình bình hành
\(AB = AD = 2\,cm.\) Vậy tứ giác \(ABCD\) là hình thoi
Lại có: \(BD = 3\,cm\)
Hình thoi dựng được thỏa mãn điều kiện bài toán.
soanvan.me
