Đề bài
Cho tam giác \(ABC\) vuông cân tại \(A.\) Trên cạnh \(BC\) lấy các điểm \(H,\, G\) sao cho \(BH = HG = GC.\) Qua \(H\) và \(G\) kẻ các đường vuông góc với \(BC,\) chúng cắt \(AB\) và \(AC\) theo thứ tự ở \(E\) và \(F.\) Tứ giác \(EFGH\) là hình gì ? Vì sao ?
Phương pháp giải - Xem chi tiết
Vận dụng kiến thức :
- Tứ giác có một cặp cạnh đối song song và bằng nhau là hình bình hành.
- Hình bình hành có một góc vuông là hình chữ nhật.
- Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông.
Lời giải chi tiết
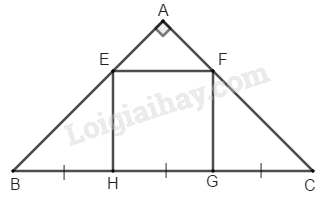
Vì \(∆ ABC\) vuông cân tại \(A\) \( \Rightarrow \widehat B = \widehat C = {45^0}\)
Vì \(∆ BHE\) vuông tại \(H\) có \(\widehat B = {45^0}\)
\(⇒ ∆ BHE\) vuông cân tại \(H\) nên \(HB = HE\)
Vì \(∆ CGF\) vuông tại \(G\) có \(\widehat C = {45^0}\)
\(⇒ ∆ CGF\) vuông cân tại \(G\) nên \(GC = GF\)
Ta có: \(BH = HG = GC\) (gt)
Suy ra: \(HE = HG = GF\)
Ta có \(EH // GF\) (hai đường thẳng cùng vuông góc với đường thẳng BC)
Nên tứ giác \(HEFG\) là hình bình hành (vì có một cặp cạnh đối song song bằng nhau)
Lại có \(\widehat {EHG} = {90^0}\) do đó \(HEFG\) là hình chữ nhật
Mà \(EH = HG\) (chứng minh trên)
Vậy \(HEFG\) là hình vuông.
soanvan.me
