Đề bài
Cho hình vuông \(ABCD.\) Trên cạnh \(AD\) lấy điểm \(F,\) trên cạnh \(DC\) lấy điểm \(E\) sao cho \(AF = DE.\) Chứng minh rằng \(AE = BF\) và \(AE ⊥ BF.\)
Phương pháp giải - Xem chi tiết
- Vận dụng kiến thức về các trường hợp bằng nhau của tam giác.
- Áp dụng định lí: Tổng ba góc trong một tam giác bằng \(180^0\)
Lời giải chi tiết
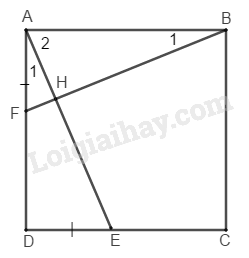
Xét \(∆ ABF\) và \(∆ DAE:\)
\(AB = DA\) (gt)
\(\widehat {BAF} = \widehat {ADE} = {90^0}\)
\(AF = DE\) (gt)
Do đó: \(∆ ABF = ∆ DAE\, (c.g.c)\)
\(⇒ BF = AE\) và \({\widehat B_1} = {\widehat A_1}\)
Gọi \(H\) là giao điểm của \(AE\) và \(BF.\)
\(\widehat {BAF} = {\widehat A_1} + {\widehat A_2} = {90^0}\)
Suy ra: \({\widehat B_1} + {\widehat A_2} = {90^0}\)
Trong \(∆ ABH\) ta có:
\(\widehat {AHB} + {\widehat B_1} + {\widehat A_2} = {180^0}\)
\(\widehat {AHB} = {180^0} - \left( {{{\widehat B}_1} + {{\widehat A}_2}} \right)\)\( = {180^0} - {90^0} = {90^0}\)
Vậy \(AE ⊥ BF\).
soanvan.me
