Đề bài
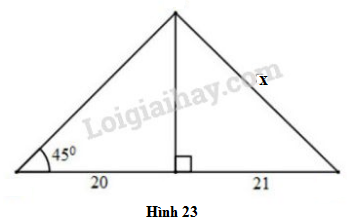
Tìm giá trị của \(x\) trong hình \(23\):
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
+) Sử dụng tỷ số lượng giác: \(\tan \alpha = \dfrac{cạnh\ đối}{cạnh\ kề} \Rightarrow {cạnh\ đối}=\tan \alpha . {cạnh\ kề}\).
+) Dùng định lí Pytago trong tam giác vuông biết hai cạnh góc vuông, tính được cạnh huyền.
Lời giải chi tiết
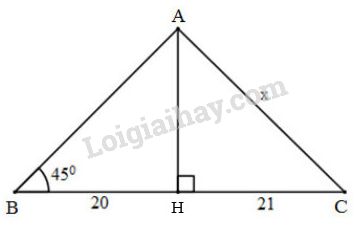
Vẽ lại hình và đặt tên các góc như hình sau:
Cách 1:
Xét tam giác \(BHA\) vuông tại \(H\) có \( \widehat{B} = 45^o\), \(BH=20\) nên:
\(\tan B=\dfrac{AH}{BH} \Leftrightarrow \tan 45^o =\dfrac{AH}{20}\)
\(\Leftrightarrow AH=20. \tan 45^o = 20\)
Áp dụng định lí Pytago vào tam giác \(AHC\) vuông tại \(H\), ta có:
\(AC=\sqrt{AH^2+HC^2}=\sqrt{20^2+21^2}=29\)
Vậy \(x=29\)
Cách 2:
Tam giác ABH vuông tại H có 1 góc bằng \(45^0\) nên tam giác ABH vuông cân tại H
\(\Rightarrow AH = BH\), mà BH = 20 nên AH = 20
Áp dụng định lí Pytago vào tam giác \(AHC\) vuông tại \(H\), ta có:
\(AC=\sqrt{AH^2+HC^2}=\sqrt{20^2+21^2}=29\)
Vậy \(x=29\)
