Đề bài
Cho đường thẳng \(d\), điểm \(A\) nằm trên đường thẳng \(d\), điểm \(B\) nằm ngoài đường thẳng \(d\). Hãy dựng đường tròn \((O)\) đi qua điểm \(B\) và tiếp xúc với đường thẳng \(d\) tại \(A.\)
Phương pháp giải - Xem chi tiết
Vận dụng định lí : Nếu đường thẳng đi qua một điểm của đường tròn và vuông góc với bán kính đi qua điểm đó thì đường thẳng là một tiếp tuyến của đường tròn.
Lời giải chi tiết
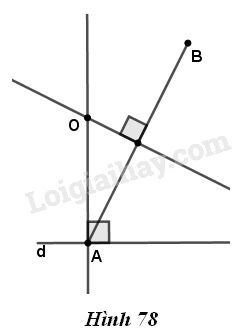
a) Cách dựng
- Dựng đường trung trực của \(AB.\)
- Dựng đường vuông góc với đường thẳng \(d\) tại \(A.\)
- Hai đường thẳng trên cắt nhau tại \(O.\)
- Dựng đường tròn \(\left( {O;OA} \right)\)
b) Chứng minh :
- Điểm \(O\) thuộc đường trung trực của \(AB\) nên đường tròn \(\left( {O;OA} \right)\) đi qua \(A\) và \(B.\)
- Đường thẳng \(d\) vuông góc với bán kính \(OA\) nên \(d\) là tiếp tuyến của \(\left( {O;OA} \right).\)
soanvan.me
