Đề bài
Cho đường tròn \((O)\), dây \(AB\) khác đường kính. Qua \(O\) kẻ đường vuông góc với \(AB\), cắt tiếp tuyến tại \(A\) của đường tròn ở điểm \(C\).
a) Chứng minh rằng \(CB\) là tiếp tuyến của đường tròn.
b) Cho bán kính của đường tròn bằng \(15cm,\ AB=24cm\). Tính độ dài \(OC.\)
Phương pháp giải - Xem chi tiết
a) Vận dụng kiến thức : Nếu đường thẳng đi qua một điểm của đường tròn và vuông góc với bán kính đi qua điểm đó thì đường thẳng là một tiếp tuyến của đường tròn.
b) Vận dụng định lí “Đường kính vuông góc với dây thì đi qua trung điểm của dây đó. Tìm \(AH.\)
- Tìm \(OH\)
- Áp dụng hệ thức lượng giữa cạnh góc vuông và đường cao để tìm \(OC.\)
Lời giải chi tiết
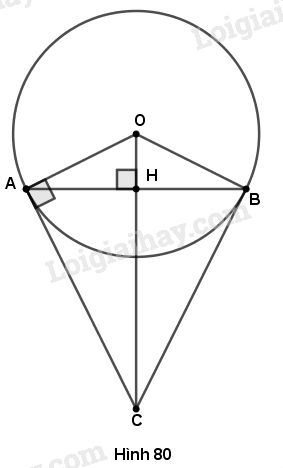
a) Gọi \(H\) là giao điểm của \(OC\) và \(AB.\)
Tam giác \(AOB\) cân tại \(O\) có \(OH\) là đường cao nên cũng là tia phân giác của góc \(AOB,\) do đó \(\widehat {AOH} = \widehat {BOH}.\)
Xét tam giác \(OBC\) và tam giác \(OAC,\) ta có:
\(OA = OB\) (đều bằng bán kính của đường tròn)
\(OC\) là cạnh chung
\(\widehat {AOH} = \widehat {BOH}\) (chứng minh trên)
Do đó, \(\Delta OBC = \Delta OAC\left( {c.g.c} \right)\)
Suy ra \(\widehat {OBC} = \widehat {OAC}.\)
Ta có \(\widehat {OAC} = {90^o}\) (vì \(AC\) là tiếp tuyến của \(\left( O \right)\)) nên \(\widehat {OBC} = {90^o}.\)
Đường thẳng \(CB\) đi qua một điểm thuộc đường tròn và vuông góc với bán kính tại điểm đó nên \(CB\) là tiếp tuyến của \(\left( O \right)\)
b) Để tính \(OC,\) ta cần tính \(OH.\) Do đó trước tiên ta tính \(AH:\)
Ta có \(OH \bot AB\) nên \(AH = HB = \dfrac{1}{2}AB = 24:2 = 12\left( {cm} \right).\)
Tính \(OH:\) Áp dụng định lí Py-ta-go vào tam giác vuông \(AHO,\) ta có \(O{H^2} = O{A^2} - A{H^2} = {15^2} - {12^2} = 81\) nên \(OH = 9cm.\)
Tam giác \(AOC\) vuông tại \(A\) với đường cao \(AH\) nên \(O{A^2} = OC.OH\) tức là \({15^2} = OC.9\)
Do đó \(OC = \dfrac{{225}}{9} = 25\left( {cm} \right).\)
soanvan.me
