Đề bài
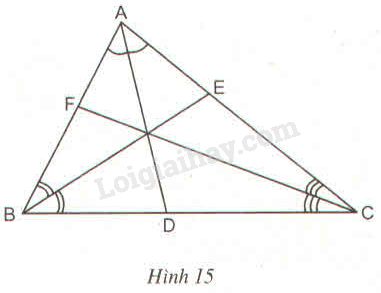
Tam giác \(ABC\) có các đường phân giác \(AD, BE\) và \(CF\) (h15).
Chứng minh rằng:
\(\displaystyle {{DB} \over {DC}}.{{EC} \over {EA}}.{{FA} \over {FB}} = 1\)
Phương pháp giải - Xem chi tiết
Sử dụng tính chất đường phân giác: Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn tỉ lệ với hai cạnh kề của hai đoạn ấy.
Lời giải chi tiết
Áp dụng tính chất đường phân giác vào \(\Delta ABC\)
Đường phân giác \(AD\) của \(\widehat {BAC}\) ta có:
\(\displaystyle {{DB} \over {DC}} = {{AB} \over {AC}}\) (1)
Đường phân giác \(BE\) của \(\widehat {ABC}\) ta có:
\(\displaystyle{{EC} \over {EA}} = {{BC} \over {AB}}\) (2)
Đường phân giác \(CF\) của \(\widehat {ACB}\) ta có:
\(\displaystyle {{FA} \over {FB}} = {{CA} \over {CB}}\) (3)
Nhân từng vế (1), (2) và (3), ta được:
\(\displaystyle {{DB} \over {DC}}.{{EC} \over {EA}}.{{FA} \over {FB}} = {{AB} \over {AC}}.{{BC} \over {AB}}.{{CA} \over {CB}} \)\(\,= 1\).
soanvan.me
