Đề bài
Tam giác \(ABC\) vuông tại \(A\) có đường phân giác \(AD\). Biết rằng độ dài của các cạnh góc vuông \(AB = 3,75cm, AC = 4,5cm\)
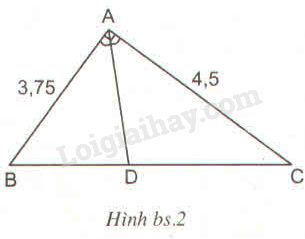
Hãy chọn kết quả đúng (tính chính xác đến chữ số thập phân).
1) Độ dài của đoạn thẳng \(BD\) là:
A. \(18,58\) B. \(2,66\)
C. \(2,65\) D. \(3,25\)
2) Độ dài đoạn thẳng \(CD\) là:
A. \(27,13\) B. \(2,68\)
C. \(3,2\) D. \(3,15\)
Phương pháp giải - Xem chi tiết
Sử dụng:
- Tính chất đường phân giác: Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn tỉ lệ với hai cạnh kề của hai đoạn ấy.
- Định lí Pytago: Bình phương của cạnh huyền bằng tổng các bình phương của các cạnh góc vuông.
- Tính chất: \(\dfrac{a}{b} = \dfrac{c}{d} \Rightarrow \dfrac{a}{{a + b}} = \dfrac{c}{{c + d}}\)
Lời giải chi tiết
1) Áp dụng định lí Pytago vào tam giác vuông \(ABC\), ta có:
\(B{C^2} = A{B^2} + A{C^2} \)\(\,= 3,{75^2} + 4,{5^2} = 34,3125\)
\(\Rightarrow BC \approx 5,86\)
Áp dụng tính chất đường phân giác của tam giác vào \(\Delta ABC\), phân giác \(AD\) ta có:
\(\dfrac{{BD}}{{CD}} = \dfrac{{AB}}{{AC}} = \dfrac{{3,75}}{{4,5}} = \dfrac{5}{6}\)
Từ đó, ta có:
\(\begin{array}{l}
\dfrac{{BD}}{{CD}} = \dfrac{5}{6}\\
\Rightarrow \dfrac{{BD}}{{BD + CD}} = \dfrac{5}{{5 + 6}}\\
\Rightarrow \dfrac{{BD}}{{BC}} = \dfrac{5}{{11}}
\end{array}\)
\(\Rightarrow BD = \dfrac{5}{{11}}.BC\)\(\, = \dfrac{5}{{11}}.5,86 = 2,66\,\left( {cm} \right)\)
Chọn B.
2) Ta có \(CD = BC - BD = 5,86 - 2,66\)\(\, = 3,2\).
Chọn C.
soanvan.me
