Bài 21 trang 88 SBT toán 8 tập 2

Đề bài

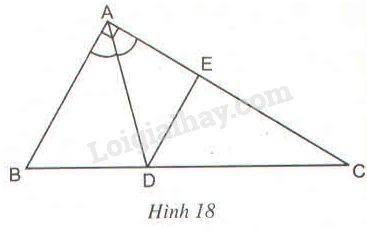
Cho tam giác vuông \(ABC\) (\(\widehat A = {90^0}\)), \(AB = 21cm, AC = 28cm;\) đường phân giác góc \(A\) cắt \(BC\) tại \(D,\) đường thẳng qua \(D\) và song song với \(AB\), cắt \(AC\) tại \(E\) (h18).

a) Tính độ dài các đoạn thẳng \(BD, DC\) và \(DE.\)

b) Tính diện tích tam giác \(ABD\) và diện tích tam giác \(ACD.\)

Lời giải chi tiết

a) Áp dụng định lí Py-ta-go vào tam giác vuông \(ABC\), ta có:

\(B{C^2} = A{B^2} + A{C^2} = {21^2} + {28^2} \)\(\,= 1225\)

\( \Rightarrow  BC = 35 \;(cm)\)

Vì \(AD\) là đường phân giác của \(\widehat {BAC}\) nên ta có:

\(\displaystyle {{BD} \over {DC}} = {{AB} \over {AC}}\) (tính chất đường phân giác)

Áp dụng tính chất mở rộng của tỉ lệ thức ta có:

\(\displaystyle {{BD} \over {DC}} = {{AB} \over {AC}}\)

\( \displaystyle \Rightarrow {{BD} \over {BD + DC}} = {{AB} \over {AB + AC}}\)

\( \displaystyle \Rightarrow {{BD} \over {BC}} = {{AB} \over {AB + AC}}\)

\( \displaystyle \Rightarrow  BD = {{BC.AB} \over {AB + AC}} = {{35.21} \over {21 + 28}} = 15\) (cm)

Vậy \(DC = BC - BD = 35 - 15 = 20\)\( \;(cm)\)

Trong tam giác \(ABC\) có \(DE // AB\) nên theo hệ quả của định lí Ta-lét ta có:

\(\displaystyle {{DC} \over {BC}} = {{DE} \over {AB}}\)

\( \displaystyle \Rightarrow DE = {{DC.AB} \over {BC}} = {{20.21} \over {35}} = 12\) (cm)

b) Ta có \( \displaystyle  {S_{ABC}} = {1 \over 2}AB.AC = {1 \over 2}.21.28 = 294\)\(\;(c{m^2})\)

Vì \(∆ ABC\) và \(∆ ADB\) có chung đường cao kẻ từ đỉnh \(A\), do đó:

\(\displaystyle {{{S_{ADB}}} \over {{S_{ABC}}}} = {{BD} \over {BC}} = {{15} \over {35}} = {3 \over 7} \)

\(\displaystyle   \Rightarrow {S_{ADB}} = {3 \over 7}{S_{ABC}} = {3 \over 7}.294 = 126\)\(\;(c{m^2})  \)

Vậy \({S_{ADC}} = {S_{ABC}} - {S_{ADB}} = 294 - 126 \)\(\,= 168\;(c{m^2})\).

soanvan.me