Đề bài
Cho hình thoi \(ABCD\) có \(\widehat A = {60^0}\). Gọi \(E, F, G, H\) lần lượt là trung điểm của các cạnh \(AB, BC, CD, DA\). Chứng minh rằng đa giác \(EBFGDH\) là lục giác đều.
Phương pháp giải - Xem chi tiết
Áp dụng:
- Hình thoi có tất cả các cạnh bằng nhau,
- Lục giác đều là hình có sáu cạnh bằng nhau và sáu góc bằng nhau.
Lời giải chi tiết
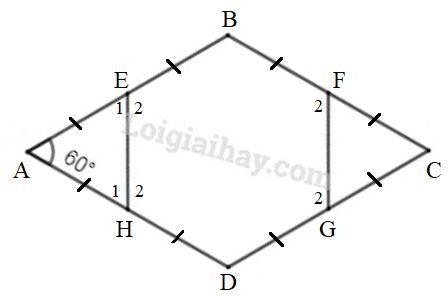
Ta có \(AE=BE, BF=CF,CG=DG,\)\(\,DH=AH\) và \(AB = BC = CD = DA\) (cạnh hình thoi) nên \(AE = EB = BF = FC = CG = GD\)\(\, = DH = HA\)
\(\Delta AEH\) có \(AE=AH\) và \(\widehat A = {60^o}\) nên là tam giác đều, suy ra \(EH=EB\)
Chứng minh tương tự ta có \(FG=BF\)
Suy ra \(HE=EB= BF=FG=GD=DH\), tức là lục giác \(EBFGDH\) có sáu cạnh bằng nhau. (1)
Tam giác \( AEH\) đều nên \(\widehat {{E_1}} = \widehat {{H_1}} = {60^o}\) suy ra \(\widehat {{E_2}} = \widehat {{H_2}} = {120^o}\).
Chứng minh tương tự ta có \(\widehat {{F_2}} = \widehat {{G_2}} = {120^o}\)
Ta có \(\widehat A + \widehat B = {180^o}\) (vì \(BC//AD\)) nên \(\widehat B = {180^o} - \widehat A = {180^o} - {60^o} = {120^o}\). Suy ra \(\widehat D = {120^o}\)
Lục giác \(EBFGDH\) có sáu góc bằng nhau (bằng \(120^o\)) (2)
Từ (1) và (2) suy ra \(EBFGDH\) là lục giác đều.
soanvan.me
