Câu 1.
Tổng số đo các góc của đa giác \(14\) cạnh bằng
(A) \(24v\) (B) \(28v\)
(C) \(20v\) (D) \(14v\)
Phương pháp giải:
Sử dụng: Tổng số đo các góc của đa giác \(n\) cạnh bằng \((n-2).2v\).
Giải chi tiết:
Tổng số đo các góc của đa giác \(14\) cạnh bằng \((14-2).2v=24v\)
Chọn A.
Câu 2.
Một đa giác có tổng số đo góc bằng \(900^o\). Số cạnh của đa giác đó là
(A) \(9\) (B) \(7\)
(C) \(6\) (D) \(5\).
Phương pháp giải:
Sử dụng: Tổng số đo các góc của đa giác \(n\) cạnh bằng \((n-2).180^o\).
Giải chi tiết:
Gọi số cạnh của đa giác cần tìm là \(n\) cạnh \((n\in \mathbb N^*)\)
Tổng số đo các góc của đa giác bằng \(900^o\) nên ta có:
\(\;\;(n-2).180^o=900^o\)
\(\eqalign{
& \Rightarrow n - 2 = {900^o}:{180^o} = 5 \cr
& \Rightarrow n = 5 + 2 = 7 \cr} \)
Chọn B.
Câu 3.
Đúng ghi Đ, sai ghi S vào ô trống
a) Hình thoi là một tứ giác đều.
b) Hình chữ nhật là một tứ giác đều.
c) Hình vuông là một tứ giác đều.
Phương pháp giải:
Áp dụng định nghĩa: Đa giác đều là đa giác có tất cả các cạnh bằng nhau và tất cả các góc bằng nhau.
Giải chi tiết:
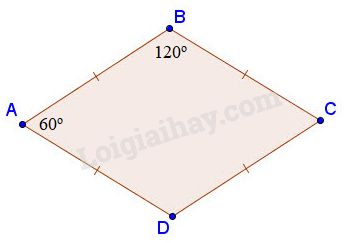
a) S. Hình thoi có tất cả các cạnh bằng nhau như chưa chắc tất cả các góc đã bằng nhau.
VD:
Hình thoi có \(\widehat A = {60^o}, \widehat B = {120^o}\) có tất cả các cạnh bằng nhau, nhưng không có tất cả các góc bằng nhau nên không là tứ giác đều.
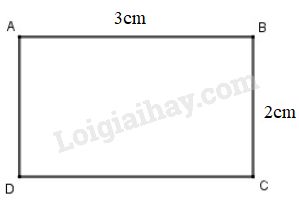
b) S. Hình chữ nhật có tất cả các góc bằng nhau nhưng các cạnh chưa chắc đã bằng nhau.
VD:
Hình chữ nhật \(ABCD\) có \(AB=3cm, BC=2cm\) có tất cả các góc bằng nhau, nhưng không có tất cả các cạnh bằng nhau nên không là tứ giác đều.
c) Đ. Hình vuông có tất cả các cạnh và các góc bằng nhau.
soanvan.me
