Đề bài
Cho hai đường tròn bằng nhau \((O)\) và \((O')\) cắt nhau tại \(A\) và \(B\). Vẽ đường thẳng qua \(A\) cắt \(O\) tại \(M\) và cắt \((O')\) tại \(N\) ( \(A\) nằm giữa \(M\) và \(N\)). Hỏi \(MBN\) là tam giác gi? Tại sao?
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Các góc nội tiếp cùng chắn một cung hoặc chắn các cung bằng nhau thì bằng nhau.
Lời giải chi tiết
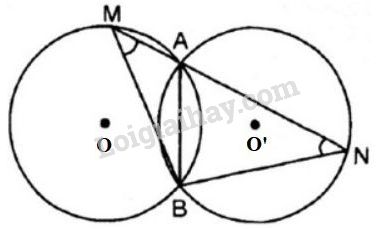
Vì hai đường tròn \(\left( O \right)\) và \(\left( {O'} \right)\) bằng nhau nên cung \(AB\) của \(\left( O \right)\) và \(\left( {O'} \right)\) bằng nhau
Suy ra \(\widehat {AMB} = \widehat {ANB}\) (các góc nội tiếp chắn các cung bằng nhau thì bằng nhau)
Do đó tam giác \(BMN\) là tam giác cân tại \(B.\)
soanvan.me
