Chứng minh rằng:
LG a
\(\int\limits_0^1 {f\left( x \right)} dx = \int\limits_0^1 {f\left( {1 - x} \right)dx.} \)
Phương pháp giải:
Đổi biến u=1-x
Lời giải chi tiết:
Đặt \(u = 1 - x \Rightarrow du = - dx\)
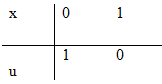
\(\int\limits_0^1 {f\left( x \right)} dx = \int\limits_1^0 {f\left( {1 - u} \right)} \left( { - du} \right) \) \(= \int\limits_0^1 {f\left( {1 - u} \right)} du = \int\limits_0^1 {f\left( {1 - x} \right)} dx\)
(Do \(\int\limits_a^b {f\left( u \right)du} = \int\limits_a^b {f\left( v \right)dv} \))
LG b
\(\int\limits_{ - 1}^1 {f\left( x \right)} dx = \int\limits_0^1 {\left[ {f\left( x \right) + f\left( { - x} \right)} \right]} dx.\)
Lời giải chi tiết:
\(\int\limits_{ - 1}^1 {f\left( x \right)} dx = \int\limits_{-1}^0 {f\left( x \right)} dx + \int\limits_0^1 {f\left( x \right)} dx\) với \(\int\limits_{ - 1}^0 {f\left( x \right)} dx\)
Đặt \(u = - x \Rightarrow du = - dx\).
Đổi cận \(x = - 1 \Rightarrow u = 1,x = 0 \Rightarrow u = 0\)
Khi đó \(\int\limits_{ - 1}^0 {f\left( x \right)dx = \int\limits_1^0 {f\left( { - u} \right)} } \left( { - du} \right) \) \(= \int\limits_0^1 {f\left( { - u} \right)} du = \int\limits_0^1 {f\left( { - x} \right)} dx\)
Do đó \(\int\limits_{ - 1}^1 {f\left( x \right)dx} = \int\limits_0^1 {f\left( { - x} \right)dx} + \int\limits_0^1 {f\left( x \right)dx} \) \(= \int\limits_0^1 {\left[ {f\left( x \right) + f\left( { - x} \right)} \right]dx} \)
soanvan.me
