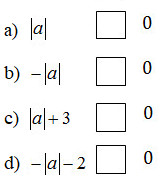Đề bài
Cho \(a\) là số bất kì, hãy đặt dấu “\(<, \,>, \,≤, \,≥\)” vào ô vuông cho đúng:
Phương pháp giải - Xem chi tiết
- Áp dụng các tính chất liên hệ giữa thứ tự và phép nhân với số dương và số âm, liên hệ giữa thứ tự và phép cộng.
- Áp dụng tính chất của giá trị tuyệt đối \(\left| a \right| ≥ 0 \) với mọi \(a.\)
Lời giải chi tiết
a) Với \(a=0\) thì \(\left| a \right| = 0 \).
Với \(a\ne0\) thì \(\left| a \right| > 0 \)
Vậy với mọi \(a\) thì \(\left| a \right| ≥ 0 .\)
b) Ta có : \(\left| a \right| ≥ 0 \)
\(\Rightarrow (-1) .\left| a \right| ≤ (-1).0 \) (Nhân số \(-1\) vào hai vế của bất đẳng thức \(\left| a \right| ≥ 0 \)).
Hay \(-\left| a \right| \le 0 .\)
c) - Nếu \(a = 0\), ta có \(\left| a \right| = 0\)
Khi đó \(\left| a \right| + 3 = 3>0,\)
- Nếu \(a ≠ 0\), ta có \(\left| a \right| > 0\) , suy ra \(\left| a \right| + 3 > 3\) \((1)\)
Lại có : \( 3 > 0\) \((2)\)
Từ \((1)\) và \((2)\), theo tính chất bắc cầu ta có \(\left| a \right| + 3 > 0\)
Vậy : \(\left| a \right| + 3 > 0\) với \(a\) bất kì.
d) Theo câu b) ta có : \(-\left| a \right| \le 0 \)
- Nếu \(a = 0\), ta có \(\left| a \right| = 0\)
Khi đó \(-\left| a \right| - 2 = -2<0.\)
- Nếu \(a ≠ 0\), ta có \(\left| a \right| > 0\) , suy ra \(-\left| a \right| <0\)
\(\Rightarrow -\left| a \right| + (-2 )< 0+(-2 ) \)
\(\Rightarrow -\left| a \right| -2 < -2 \) \((3)\)
Lại có : \( -2 < 0\) \((4)\)
Từ \((3)\) và \((4)\), theo tính chất bắc cầu ta có \(-\left| a \right| -2 < 0.\)
Vậy : \(-\left| a \right| -2< 0\) với \(a\) bất kì.
soanvan.me