Đề bài
Vẽ hình biểu diễn của một hình lục giác đều.
Phương pháp giải - Xem chi tiết
Cách vẽ hình biểu diễn của một hình \(H\) cho trước:
a) Xác định các yếu tố song song của hình \(H\).
b) Xác định tỉ số điểm \(M\) chia đoạn \(AB\).
c) Hình \(H'\) là hình biểu diễn của \(H\) có tính chất sau:
- Bảo đảm tính song song của hình \(H\).
- Bảo đảm tỉ số của điểm \(M\) chia đoạn \(AB\).
Trong bài này ta sử dụng tính chất:
- Một hình bình hình bất kỳ có thể coi là hình biểu diễn của một hình bình hành tùy ý cho trước (có thể là hình bình hành, hình vuông, hình chữ nhật, hình thoi...).
- Hình lục giác đều có tâm đối xứng là giao điểm của các đường chéo.
- Tính chất đối xứng tâm.
Lời giải chi tiết
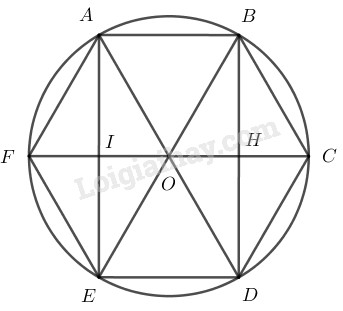
Với hình lục giác đều \(ABCDEF\) ta nhận thấy:
- Tứ giác \(OABC\) là hình bình hành (vừa là hình thoi);
- Các điểm \(D\), \(E\), \(F\) lần lượt là các điểm đối xứng của các điểm \(A\), \(B\), \(C\) qua tâm \(O\).
Từ đó suy ra cách vẽ hình biểu diễn của lục giác đều \(ABCDEF\) như sau:
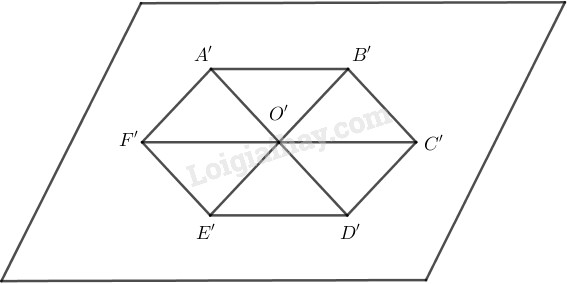
- Vẽ hình bình hành \(O’A’B’C’\) biểu diễn cho hình bình hành \(OABC\).
- Lấy các điểm \(D’\), \(E’\), \(F’\) lần lượt đối xứng của \(A’\), \(B’\), \(C’\) qua tâm \(O’\), ta được hình biểu diễn \(A’B’C’D’E’F’\) của hình lục giác đều \(ABCDEF\).
Chú ý. Ta có thể vẽ hình biểu diễn hình lục giác đều dựa trên sự phân tích sau đây ở hình thực \(ABCDEF\):
- Tứ giác \(ABDE\) là hình chữ nhật;
- Gọi \(I\) là trung điểm của cạnh \(AE\) và \(H\) là trung điểm của cạnh \(BD\);
- Các điểm \(F\) và \(C\) đối xứng của \(O\) lần lượt qua \(I\) và \(H\).
Từ đó ta có cách vẽ sau đây:
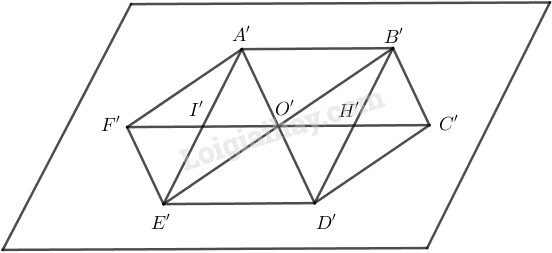
- Vẽ hình bình hành \(A’B’D’E’\) biểu diễn cho hình chữ nhật \(ABDE\)
- Gọi \(I’\) và \(H’\) lần lượt là trung điểm của \(A’E’\)và \(B’D’\).
- Gọi \(F’\) đối xứng với \(O’\) qua \(I’\) và (C’\) đối xứng với \(O’\) qua \(H’\), ta được hình biểu diễn \(A’B’C’D’E’F’\) của hình lục giác đều.
soanvan.me
