Đề bài
Hãy vẽ hình biểu diễn của một đường tròn cùng với hai đường kính vuông góc của đường tròn đó.
Phương pháp giải - Xem chi tiết
Cách vẽ hình biểu diễn của một hình \(H\) cho trước:
a) Xác định các yếu tố song song của hình \(H\).
b) Xác định tỉ số điểm \(M\) chia đoạn \(AB\).
c) Hình \(H'\) là hình biểu diễn của \(H\) có tính chất sau:
- Bảo đảm tính song song của hình \(H\).
- Bảo đảm tỉ số của điểm \(M\) chia đoạn \(AB\).
Trong bài này ta sử dụng tính chất:
- Hình elip để biểu diễn hình tròn.
- Phép chiếu song song biến ba điểm thẳng hàng thành ba điểm thẳng hàng và không làm thay đổi thứ tự của ba điểm đó. Bảo toàn tỉ số của điểm chia đoạn.
Lời giải chi tiết
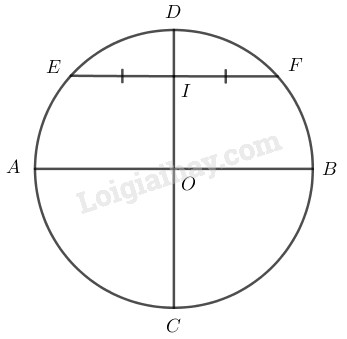
Giả sử trên hình thực ta có đường tròn tâm \(O\) cùng với hai đường kính vuông góc của đường tròn đó là \(AB\) và \(CD\).
Ta vẽ thêm một dây cung \(EF\) song song với \(AB\).
Khi đó đường kính \(CD\) sẽ đi qua trung điểm \(I\) của đoạn \(EF\).
Từ đó ta suy ra cách vẽ sau đây:
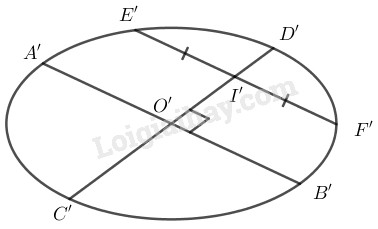
- Vẽ hình elip biểu diễn cho đường tròn và vẽ đường kính \(A’B’\) của hình elip đó. Đường kính này đi qua tâm \(O’\) của elip.
- Vẽ một dây cung \(E’F’\) song song với đường kính \(A’B’\).
- Gọi \(I’\) là trung điểm của \(E’F’\). Đường thẳng \(O’I’\) cắt elip tại hai điểm \(C’\) và \(D’\). Ta có \(A’B’\) và \(C’D’\) là hình biểu diễn của hai đường kính vuông góc với nhau của đường tròn.
Nhận xét. Hình bình hành \(A’C’B’D’\) là hình biểu diễn của hình vuông \(ACBD\) nội tiếp trong một đường tròn.
soanvan.me
