Đề bài
Hãy chọn phép chiếu song song với phương chiếu và mặt phẳng chiếu thích hợp để hình chiếu song song của một tứ diện cho trước là một hình bình hành.
Phương pháp giải - Xem chi tiết
Cách vẽ hình biểu diễn của một hình \(H\) cho trước:
a) Xác định các yếu tố song song của hình \(H\).
b) Xác định tỉ số điểm \(M\) chia đoạn \(AB\).
c) Hình \(H'\) là hình biểu diễn của \(H\) có tính chất sau:
- Bảo đảm tính song song của hình \(H\).
- Bảo đảm tỉ số của điểm \(M\) chia đoạn \(AB\).
Trong bài này ta sử dụng tính chất: Phép chiếu song song biến ba điểm thẳng hàng thành ba điểm thẳng hàng và không làm thay đổi thứ tự của ba điểm đó. Bảo toàn tỉ số của điểm chia đoạn.
Lời giải chi tiết
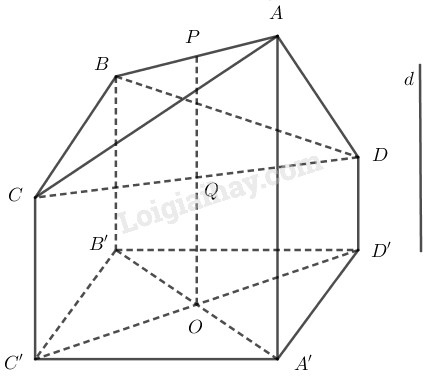
Cho tứ diện \(ABCD\). Gọi \(d\) là một đường thẳng không song song với với các cạnh của tứ diện và \(\left( \alpha \right)\) là một mặt phẳng cắt \(d\). Gọi \(A’\), \(B’\), \(C’\), \(D’\) lần lượt là hình chiếu của \(A\), \(B\), \(C\), \(D\) trên mặt phẳng \(\left( \alpha \right)\). Gọi \(P\) và \(Q\) lần lượt là trung điểm của hai cạnh đối diện \(AB\) và \(CD\). Khi đó hình chiếu của \(P’\) và \(Q’\) của \(P\) và \(Q\) sẽ lần lượt là trung điểm của \(A’B’\) và \(C’D’\).
Muốn cho \(A’\), \(B’\), \(C’\), \(D’\) là các đỉnh của một hình bình hành ta chỉ cần chọn phương chiếu d sao cho \(d\) song song với đường thẳng \(PQ\).
Vậy để hình chiếu song song của một tứ diện là một hình bình hành ta có thể chọn :
- Phương chiếu d là phương của một trong ba đường thẳng đi qua trung điểm của hai cạnh đối diện của tứ diện cho trước.
- Mặt phẳng chiếu \(\left( \alpha \right)\) là mặt phẳng tùy ý, nhưng phải cắt đường thẳng \(d\).
soanvan.me
