Đề bài
Hai đường tròn \((O)\) và \((O’)\) cắt nhau tại \(A\) và \(B.\) Qua \(A\) vẽ cát tuyến \(CAD\) với hai đường tròn \((C\in (O),\) \(D \in (O’)).\)
\(a)\) Chứng minh rằng khi cát tuyến quay xung quang điểm \(A\) thì \(\widehat {CBD}\) có số đo không đổi.
\(b)\) Từ \(C\) và \(D\) vẽ hai tiếp tuyến với đường tròn. Chứng minh rằng hai tiếp tuyến này hợp với nhau một góc có số đo không đổi khi cát tuyến \(CAD\) quay xung quanh điểm \(A.\)
Phương pháp giải - Xem chi tiết
Ta sử dụng kiến thức:
+) Trong một đường tròn, số đo góc nội tiếp bằng nửa số đo của cung bị chắn.
+) Trong một đường tròn, góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn một cung thì bằng nhau.
Lời giải chi tiết
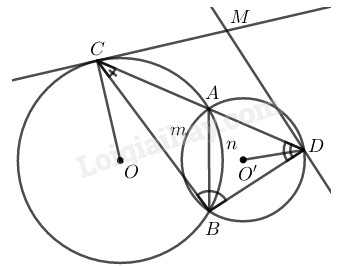
\(a)\) Ta có:
\(\widehat{ACB}=\dfrac{1}{2}sđ \overparen{AnB}\) (góc nội tiếp trong đường tròn \((O))\)
\(\widehat{ADB}=\dfrac{1}{2}sđ \overparen{AmB}\) (góc nội tiếp trong đường tròn \((O'))\)
Vì điểm \(A, B\) cố định nên \(sđ \overparen{AnB},\) \(sđ \overparen{AmB}\) không thay đổi
Vì vậy \(\widehat {ACB},\widehat {ADB}\) có số đo không đổi.
Ta có:\(\widehat {CBD} = {180^o} - \left( {\widehat {ACB} + \widehat {ADB}} \right)\) không đổi do \(\widehat {ACB},\widehat {ADB}\) có số đo không đổi.
Vậy số đo \(\widehat {CBD}\) luôn không đổi khi cát tuyến \(CAD\) thay đổi .
\(b)\) Trong \((O)\) ta có
\(\widehat {ABC} = \widehat {MCA}\) (hệ quả góc giữa tia tiếp tuyến và dây cung) \((1)\)
Trong \((O’)\) ta có: \(\widehat {ABD} = \widehat {MDA}\) (hệ quả góc giữa tia tiếp tuyến và dây cung) \((2)\)
Từ \((1)\) và \((2)\) suy ra: \(\widehat {MCA} + \widehat {MDA} = \widehat {ABC} + \widehat {ABD}\)\( = \widehat {CBD}\)
Hay \(\widehat {MCD} + \widehat {MDC} = \widehat {CBD}\) (không đổi do câu a)
Trong \(∆MCD\) ta có: \(\widehat {CMD} = {180^o} - \left( {\widehat {MCD} + \widehat {MDC}} \right)\)
\(={180^o} - \widehat {CBD}\)
Nên \(\widehat {CMD} \) không đổi do \(\widehat {CBD}\) không đổi.
Vậy \(\widehat {CMD} \) không đổi.
soanvan.me
