Đề bài
Cho đường tròn tâm \(O\) bán kính \(R.\) Lấy ba điểm bất kỳ \(A, B, C\) trên đường tròn \((O).\) Điểm \(E\) bất kỳ thuôc đoạn thẳng \(AB\) (và không trùng với \(A, B\)). Đường thẳng \(d\) đi qua điểm \(E\) và vuông góc với đường thẳng \(OA\) cắt đoạn thẳng \(AC\) tại điểm \(F.\) Chứng minh \(\widehat {BCF} + \widehat {BEF} = {180^o}.\)
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức:
+) Nếu một đường thẳng là tiếp tuyến của một đường tròn thì nó vuông góc với bán kính đi qua tiếp điểm.
+) Nếu một đường thẳng cùng vuông góc với hai đường thẳng thì hai đường thẳng đó song song với nhau.
+) Trong một đường tròn, góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn một cung thì bằng nhau.
+) Nếu một đường thẳng cắt hai đường thẳng song song thì tạo ra các cặp góc so le trong bằng nhau.
+) Tổng các góc trong một tứ giác bằng \(360^o.\)
Lời giải chi tiết
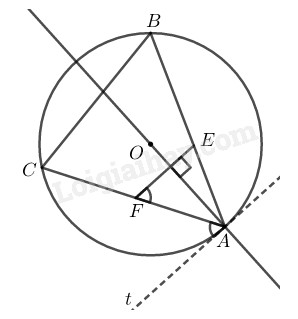
Kẻ tiếp tuyến \(At\) của đường tròn \((O)\)
Suy ra: \(At \bot OA\) (tính chất tiếp tuyến)
Mà \(EF \bot OA\) \((gt)\)
Do đó: \(At // EF\)
Nên \(\widehat {EFA} = \widehat {CAt}\) (so le trong)
Lại có: \(\widehat {CBA} = \widehat {CAt}\) (hệ quả góc giữa tia tiếp tuyến và dây cung)
Suy ra: \(\widehat {EFA} = \widehat {CBA}\) hay \(\widehat {EFA} = \widehat {CBE}\)
Mà \(\widehat {EFA} + \widehat {EFC} = {180^o}\) (hai góc kề bù)
Nên \(\widehat {CBE} + \widehat {EFC} =180^o \;\; (1)\)
Trong tứ giác \(BCFE\) ta có:
\(\widehat{BCF} +\widehat{BEF} + \widehat{CBE} +\widehat{CFE} =360^o\) (tổng các góc trong tứ giác)\( (2)\)
Từ \((1)\) và \((2)\) suy ra: \(\widehat {BCF} + \widehat {BEF} = {180^o}\)
soanvan.me
