Đề bài
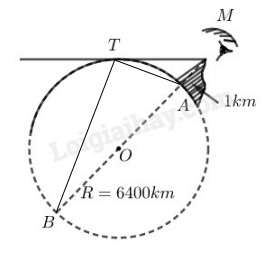
Ngồi trên một đỉnh núi cao \(1km\) thì có thể nhìn thấy một địa điểm \(T\) trên mặt đất với khoảng cách tối đa là bao nhiêu\(?\) Biết rằng bán kính trái đất gần bằng \(6400km (h.3)\)
Phương pháp giải - Xem chi tiết
Ta sử dụng kiến thức:
+) Trong một đường tròn, góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn một cung thì bằng nhau.
+) Hai tam giác đồng dạng thì ta có các cạnh tương ứng tỉ lệ.
Lời giải chi tiết
Điểm nhìn tối đa là tiếp tuyến kể từ mắt nhìn đến tiếp điểm của bề mặt Trái Đất (như hình vẽ)
Xét \(∆MTA\) và \(∆MTB,\) có:
+) \(\widehat M\) chung
+) \(\widehat {MTA} = \widehat {TBM}\) (hệ quả góc tạo bởi tiếp tuyến và dây cung)
\(\Rightarrow ∆MAT\) đồng dạng \(∆MTB\) (g.g)
\(\displaystyle {{MT} \over {MA}} = {{MB} \over {MT}}\)
\( \Rightarrow {\rm M}{{\rm T}^2} = MA.MB\)
\( \Rightarrow M{T^2} = MA\left( {MA + 2R} \right)\)(1)
Thay \(MA=1km,\)\( R = 6400 km\) vào (1), ta có: \(M{T^2} = 1\left( {1 + 2.6400} \right) = 12801\)
\( \Rightarrow MT \approx 113,1\) (km)