Đề bài
Cho tam giác \(ABC\) vuông tại \(A.\) Gọi \({V_1},{V_2},{V_3}\) theo thứ tự là thể tích của những hình sinh ra khi quay tam giác \(ABC\) một vòng xung quanh các cạnh \(BC, AB\) và \(AC.\) Chứng minh rằng:
\(\displaystyle {1 \over {V_1^2}} = {1 \over {V_2^2}} + {1 \over {V_3^2}}.\)
Phương pháp giải - Xem chi tiết
Sử dụng:
- Thể tích hình nón: \(\displaystyle V = {1 \over 3}\pi {r^2}h\).
(\(r\) là bán kính đường tròn đáy, \(h\) là chiều cao).
- Định lí Pytago trong tam giác vuông: Bình phương của cạnh huyền bằng tổng các bình phương của các cạnh góc vuông.
Lời giải chi tiết
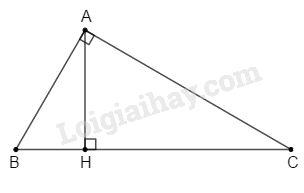
\(∆ABC\) có \(\widehat A = 90^\circ \), đặt \(AB = c, AC = b, BC = a, AH = h\); \(AH\) là đường cao kẻ từ đỉnh \(A\) đến cạnh huyền \(BC\).
Ta có: \(\displaystyle h = {{bc} \over a}\) (hệ thức lượng trong tam giác vuông)
- Khi quay tam giác vuông \(ABC\) quanh cạnh huyền \(BC\) một vòng thì cạnh \(AB\) và \(AC\) vạch nên hai hình nón có chung đáy có bán kính đáy bằng đường cao \(AH\) và tổng chiều cao \(2\) hình nón bằng cạnh huyền \(BC.\) Như vậy, thể tích hình sinh ra là:
\(\displaystyle {V_1} = {1 \over 3}\pi .A{H^2}. HB + {1 \over 3}\pi .A{H^2}.HC\)
\( \displaystyle = {1 \over 3}A{H^2}.(HB+HC) \)
\( \displaystyle = {1 \over 3}A{H^2}.BC \)
\(\displaystyle = {1 \over 3}\pi {\left( {{{bc} \over a}} \right)^2}.a = {{\pi {b^2}{c^2}} \over {3a}}\)
\( \Rightarrow \dfrac{1}{{V_1^2}} = \dfrac{1}{{{{\left( {\dfrac{{\pi {b^2}{c^2}}}{{3a}}} \right)}^2}}} = \dfrac{{9{a^2}}}{{{\pi ^2}{b^4}{c^4}}}\) (1)
- Khi quay \(∆ABC\) quanh cạnh \(AB\) một vòng ta thu được hình nón có chiều cao \(AB = c\), bán kính đáy \(AC = b\) và thể tích hình sinh ra là:
\(\displaystyle {V_2} = {1 \over 3}\pi .A{C^2}.AB = {1 \over 3}\pi {b^2}c\)
\(\displaystyle \Rightarrow {1 \over {V_2^2}} = {1 \over {\left( \displaystyle {{{\pi {b^2}c} \over 3}} \right)^2}} = {9 \over {{\pi ^2}{b^4}{c^2}}}\)
- Khi quay \(∆ABC\) quanh cạnh \(AC\) một vòng ta thu được hình nón có chiều cao \(AC = b\), bán kính đáy \(AB = c\) và thể tích hình sinh ra là:
\(\displaystyle {V_3} = {1 \over 3}{\rm{A}}{{\rm{B}}^2}.AC = {1 \over 3}\pi {c^2}b\)
\(\displaystyle \Rightarrow {1 \over {V_3^2}} = {1 \over {\left(\displaystyle {{{\pi b{c^2}} \over 3}} \right)^2}} = {9 \over {{\pi ^2}{b^2}{c^4}}}\)
Ta có:
\(\displaystyle {1 \over {V_2^2}} + {1 \over {V_3^2}} = {9 \over {{\pi ^2}{b^4}{c^2}}} + {9 \over {{\pi ^2}{b^2}{c^4}}} \)\(\,\displaystyle = {{9({b^2} + {c^2})} \over {{\pi ^2}{b^4}{c^4}}}\)
Áp dụng định lí Pytago vào \(∆ABC\) vuông tại \(A\), ta có:
\({b^2} + {c^2} = {a^2} \)
\(\displaystyle \Rightarrow {1 \over {V_2^2}} + {1 \over {V_3^2}} = {{9({b^2} + {c^2})} \over {{\pi ^2}{b^4}{c^4}}}\)\(\,\displaystyle= {{9{a^2}} \over {{\pi ^2}{b^4}{c^4}}}\) (2)
Từ (1) và (2) suy ra: \(\displaystyle {1 \over {V_1^2}} = {1 \over {V_2^2}} + {1 \over {V_3^2}}\).
soanvan.me
