Đề bài
Biểu diễn miền nghiệm của các bất phương trình sau:
a) \(3x > 2\) b) \(2y \le - 5\) c) \(2x - y \ge 1\) d) \(3x - 2y < 5\)
Phương pháp giải - Xem chi tiết
Biểu diễn miền nghiệm của bpt \(ax + by < c\)
Bước 1: Vẽ đường thẳng \(d:ax + by = c\).
Bước 2: Lấy điểm \(M\left( {{x_o};{y_o}} \right)\) không thuộc d (ta thường lấy gốc tọa độ O nếu \(c \ne 0\)). Tính \(a{x_o} + b{y_o}\) và so sánh với c
Bước 3: Kết luận
Nếu \(a{x_o} + b{y_o} < c\)thì nửa mặt phẳng (không kể đường thẳng d) chứa điểm M là miền nghiệm của bất phương trình \(ax + by < c\)
Nếu \(a{x_o} + b{y_o} > c\) thì nửa mặt phẳng (không kể d) không chứa điểm M là miền nghiệm của bất phương trình \(ax + by > c\)
Lời giải chi tiết
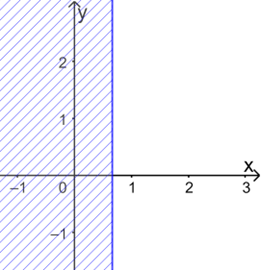
a) Vẽ đường thẳng a: \(3x = 2\)
Xét điểm O(0; 0) ta có 3.0 = 0 < 2, do đó O(0;0) không thuộc miền nghiệm của bpt \(3x > 2\).
Miền nghiệm của bất phương trình \(3x > 2\) là nửa mặt phẳng bờ a, không chứa điểm O.
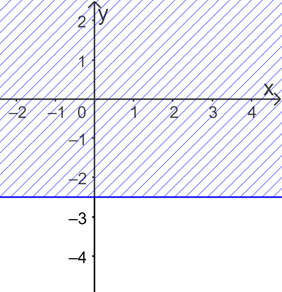
b) Vẽ đường thẳng b: 2y = – 5
Xét O(0; 0) ta có 2.0 = 0 > – 5.
=> O(0; 0) không thuộc miền nghiệm của bpt \(2y \le - 5\)
Do đó miền nghiệm của bất phương trình \(2y \le - 5\) là nửa mặt phẳng bờ b, không chứa điểm O.
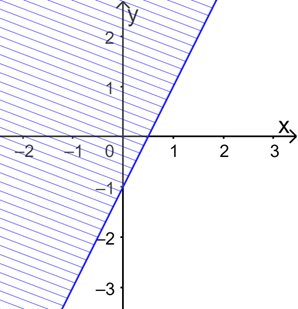
c) Vẽ đường thẳng c: 2x – y = 1
Xét điểm O(0; 0) ta có 2.0 – 0 = 0 < 1.
=> O(0; 0) không thuộc miền nghiệm của bpt \(2x - y \ge 1\)
Do đó miền nghiệm của bất phương trình \(2x - y \ge 1\) là nửa mặt phẳng bờ c, không chứa điểm O.
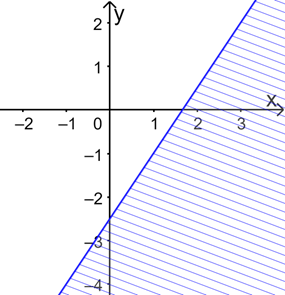
d) Vẽ đường thẳng d: 3x – 2y = 5
Xét điểm O(0; 0) ta có 3.0 – 2.0 = 0 < 5.
=> O(0; 0) thuộc miền nghiệm của bpt \(3x - 2y < 5\)
Do đó miền nghiệm của bất phương trình \(3x - 2y < 5\) là nửa mặt phẳng bờ d, chứa điểm O.